
 如图,⊙O的直径AB=2,弦AC=$\sqrt{2}$,AD=$\sqrt{3}$.
如图,⊙O的直径AB=2,弦AC=$\sqrt{2}$,AD=$\sqrt{3}$.分析 (1)直接利用圆周角定理结合AB,AC,AD的长分别得出C,D,点位置;
(2)本题大致的思路是连接BC、BD,分别在Rt△CAB和Rt△BAD中,求出∠CAD和∠CAB的度数,然后根据D点的不同位置分类讨论.
解答 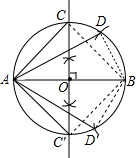 解:(1)如图所示:弦AC、AD,弦AC′、AD′即为所求;
解:(1)如图所示:弦AC、AD,弦AC′、AD′即为所求;
(2)本题分两种情况:(如图)
①当AD在AB上方时,连接BD、BC,
则∠ADB=∠ACB=90°,
Rt△ADB中,AD=$\sqrt{3}$,AB=2,
∴∠DAB=30°,
Rt△ACB中,AC=$\sqrt{2}$,AB=2,
∴∠CAB=45°,
∴∠CAD=∠CAB-∠DAB=15°,
②当AD在AB下方时,同①可求得∠CAD=75°,
综上所述:∠CAD的度数为:15°或75°.
点评 本题考查了复杂作图以及圆周角定理及直角三角形的性质,解答时要注意分两种情况讨论,不要漏解,难度适中.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是甲、乙两种固体物质在0℃-50℃之间的溶解度随温度变化的曲线图,某同学从图中获得如下几条信息,其中错误的信息是( )
如图是甲、乙两种固体物质在0℃-50℃之间的溶解度随温度变化的曲线图,某同学从图中获得如下几条信息,其中错误的信息是( )| A. | 30℃时两种固体物质的溶解度一样 | |
| B. | 在0℃-50℃之间,甲、乙两固体物质的溶解度随温度上升而增加 | |
| C. | 在0℃-40℃之间,甲、乙两固体物质溶解度相差最多是10g | |
| D. | 在0℃-50℃之间,甲的溶解度比乙的溶解度高 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A、B两点,C(4,-4),点P在y轴上,满足S△PAB=S△ABC,求点P的坐标.
如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A、B两点,C(4,-4),点P在y轴上,满足S△PAB=S△ABC,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中(以1cm为单位长度),过A(0,4)的直线垂直于y轴,点M(9,4)为直线上一点,若点P从点M出发,以每秒3cm的速度沿这条直线向左移动;点Q从原点同时出发,以每秒1cm的速度沿x轴向右移动,几秒后PQ平行于y轴( )
在平面直角坐标系中(以1cm为单位长度),过A(0,4)的直线垂直于y轴,点M(9,4)为直线上一点,若点P从点M出发,以每秒3cm的速度沿这条直线向左移动;点Q从原点同时出发,以每秒1cm的速度沿x轴向右移动,几秒后PQ平行于y轴( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,A(1,3),B(2,0),第一次将△AOB变换成△OA1B1,A1(2,3),B1(4,0);第二次将△OA1B1变换成△OA2B2,A2(4,3),B2(8,0),第三次将△OA2B2变换成△OA3B3,则B2016的横坐标为22017..
如图,在直角坐标系中,A(1,3),B(2,0),第一次将△AOB变换成△OA1B1,A1(2,3),B1(4,0);第二次将△OA1B1变换成△OA2B2,A2(4,3),B2(8,0),第三次将△OA2B2变换成△OA3B3,则B2016的横坐标为22017..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com