
【题目】为了保证安全,某仓库引进A型、B型两台机器人搬运某种有毒货物到仓库存放,这两台机器人充满电后,各能连续工作5h,按照指令,A型机器人于某日零时开始搬运,过了1h,B型机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与A型机器人搬运时间x(h)之间的关系图象,线段EF表示B种机器人的搬运量yB(kg)与A型机器人的时间x(h)之间的关系图象,根据图象提供的信息解答下列问题: 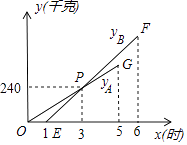
(1)点P表示的意义为:当x=3h时
(2)直接写出线段OG所表示的搬运量与时间x(h)之间的关系式
(3)A型机器人每小时搬运有毒货物kg,B型机器人每小时搬运有毒货物kg.
(4)到工作结束(各5h),A型、B型两台机器人共搬运多少有毒货物?
【答案】
(1)A型、B型各搬运有毒货物240千克
(2)yA=80x(0≤x≤5)
(3)80;120
(4)解:(80+120)×5=200×5=1000(千克)
答:A型、B型两台机器人共搬运多少有毒货物1000千克
【解析】(1)P点的含义是:当x=3h时A型、B型各搬运有毒货物240千克. 所以答案是:A种机器人搬运3小时时,A、B两种机器人的搬运量相等,且都为180千克.(2)设线段OG所表示的搬运量与时间x(h)之间的关系式为yA=kx,
将(3,240)代入yA=kx,得3k=240,
解得:k=80,
故线段OG所表示的搬运量与时间x(h)之间的关系式为yA=80x(0≤x≤5).(3)240÷3=80(kg),
240÷(3﹣1)=120(kg).
故A型机器人每小时搬运有毒货物80kg,B型机器人每小时搬运有毒货物120kg.
所以答案是:A型、B型各搬运有毒货物240千克;yA=80x(0≤x≤5);120,80.


科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.
(1)求这个二次函数的解析式并写出其图象顶点D的坐标;
(2)求∠CAD的正弦值;
(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com