
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=4,矩形DEFG的顶点D、G分别在AC、BC上,边EF在AB上.
(1)求证:△AED∽△DCG;
(2)若矩形DEFG的面积为4,求AE的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用等腰三角形的性质及正方形的性质可求得∠A=∠CDG,∠DEA=∠C,则可证得△AED∽△DCG;
(2)设AE=x,利用矩形的性质及等腰三角形的性质可求得BF=FG=DE=AE=x,从而可表示出EF,结合矩形的面积可得到关于x的方程,则可求得x的值,即可求得AE的长.
(1)证明:∵△ABC是等腰直角三角形,∠C=90°,
∴∠B=∠A=45°,
∵四边形DEFG是矩形,
∴∠AED=∠DEF=90°,DG∥AB,
∴∠CDG=∠A,
∵∠C=90°,
∴∠AED=∠C,
∴△AED∽△DCG;
(2)设AE的长为x,
∵等腰Rt△ABC中,∠C=90°,AC=4,
∴∠A=∠B=45°,AB=4![]() ,
,
∵矩形DEFG的面积为4,
∴DEFE=4,∠AED=∠DEF=∠BFG=90°,
∴BF=FG=DE=AE=x,
∴EF=4![]() -2x,
-2x,
即x(4![]() -2x)=4,
-2x)=4,
解得x1=x2=![]() .
.
∴AE的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】有一块面积为100cm2的正方形纸片.
(1)该正方形纸片的边长为 cm(直接写出结果);
(2)小丽想沿着该纸片边的方向裁剪出一块面积为90cm2的长方形纸片,使它的长宽之比为4:3.小丽能用这块纸片裁剪出符合要求的纸片吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个学校乐团,决定向某服装厂购买同样的演出服。下面是服装厂给出的演出服装的价格表:经调查:两个乐团共75人(甲乐团人数不少于40人),如果分别各自购买演出服,按每人一套的标准两个乐团共需花费5600元。请回答以下问题:
购买服装的套数 | 1~39套(含39套) | 40~79套(含79套) | 80套及以上 |
每套服装的价格 | 80元 | 70元 | 60元 |
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少人?
(3)现从甲乐团抽调a人,从乙乐团抽调b人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友,这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖。请写出所有的抽调方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
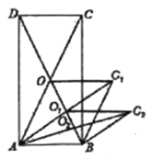
【题目】如图,矩形![]() 的面积为28,对角线交于点
的面积为28,对角线交于点![]() ;以
;以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,对角线交于点
,对角线交于点![]() ;以
;以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ;…依此类推,则平行四边形
;…依此类推,则平行四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)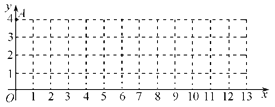
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为![]() ,则取出了多少个黑球?
,则取出了多少个黑球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com