
如图,在半径为4的圆O中,AB,CD是两条直径,M是OB的中点,CM的延长线交圆O于点E,设DE=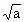 (a>0),EM=x.
(a>0),EM=x.
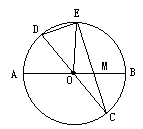
(1)用含x和a的代数式表示MC的长,并试证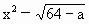 ·x+12=0;
·x+12=0;
(2)当a=15且EM>MC时,求sin∠EOM;
(3)根据图形写出EM长的取值范围;
(4)试问,在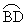 上是否存在一点E,使EM的长是关于x的方程
上是否存在一点E,使EM的长是关于x的方程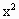 -
-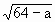 ·x+12=0的相等的实根,如果存在,求出sin∠EOM的值;如果不存在,请说明理由.
·x+12=0的相等的实根,如果存在,求出sin∠EOM的值;如果不存在,请说明理由.
|
解:(1)因为CD为圆O直径,所以∠DEC= 因为 又因为由相交弦定理EM·MC=AM·MB=12,所以MC= (2)当a=15时,方程为 因为EM>MC,所以EM=4,MC=3,由半径OE=4, 得△EOM为等腰三角形. 作EF⊥OM于F,则OF=FM=1,由勾股定理EF= (3)根据图形不难看出MB<EM<MA,所以2<EM<6. (4)假设 所以方程 因为2<EM=2 因为 所以△EOM为Rt△,∠OME= |


科目:初中数学 来源: 题型:
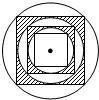 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com