
【题目】已知⊙O的半径为13,弦AB//CD,AB=24,CD=10,则AB、CD之间的距离为( )
A.17
B.7
C.12
D.7或17
【答案】D
【解析】①当弦AB和CD在圆心同侧时,如图1,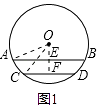
过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12﹣5=7cm;
②当弦AB和CD在圆心异侧时,如图2, 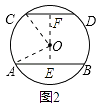
过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm,
∴AB与CD之间的距离为7cm或17cm.
故答案为:D.
此题分两种情况:①当弦AB和CD在圆心同侧时,如图1,过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,根据垂径定理得出AE=12cm,CF=5cm,根据勾股定理得出EO=5cm,OF=12cm,然后根据EF=OE-OF算出答案;②当弦AB和CD在圆心异侧时,如图2, 过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,根据垂径定理得出AE=12cm,CF=5cm,根据勾股定理得出EO=5cm,OF=12cm,然后根据EF=OE+OF算出答案 .


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 ![]() 可化为3x=6.
可化为3x=6.
D.方程 ![]() 系数化为1,得x=﹣1
系数化为1,得x=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
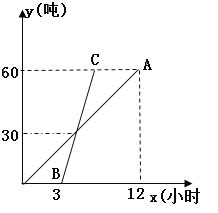
【题目】如图,是甲、乙两种机器人根据电脑程序工作时各自工作量y关于工作时间t的函数图象,线段OA表示甲机器人的工作量y1(吨)关于时间x(时)的函数图象,线段BC表示乙机器人的工作量y2(吨)关于时间a(时)的函数图象,根据图象信息回答下列填空题.
(1) 甲种机器人比乙种机器人早开始工作___ 小时,甲种机器人每小时的工作量是___吨.
(2)直线BC的表达式为 ,当乙种机器人工作5小时后,它完成的工作量是 吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点 A 在 y 轴正半轴上点 B 在 x 轴负半轴上,且 AB=2,∠BAO=15°,点 P 是线段OA 上的一个动点,则 PB ![]() PA 的最小值为_____________.
PA 的最小值为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在 ABCD 中,AC、BD 交于点 O,过点 O 的直线 l 交 AB 于 E, 交 CD 于 F,①判断 OE 和 OF 的数量关系: ,并证明;
② S四边形AEFD S四边形CFEB (填“>” 或“=” 或“<”).
(2)如图 2 是一块“L”形的材料,请你作一条直线 m,使得直线 m 两边的材料的面积相等(保留作图痕迹,不用证明).
(3)如图 3,正方形 ABCD 的边长为 2![]() cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).
cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
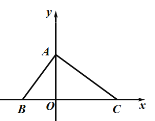
【题目】如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1) △ABC三个顶点的坐标分别为A( , ),B( , ),C( , );
(2) 是否存在点P,使得![]() ?若存在,求出满足条件的所有点P的坐标.
?若存在,求出满足条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人,1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若计划租用A型车![]() 辆,租用B型车
辆,租用B型车![]() 辆,请你设计租车方案,能一次运送所有学生,且恰好每辆车都坐满.
辆,请你设计租车方案,能一次运送所有学生,且恰好每辆车都坐满.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com