
【题目】如图,BF,CG分别是![]() 的高线,点D,E分别是BC,GF的中点,连结DF,DG,DE,
的高线,点D,E分别是BC,GF的中点,连结DF,DG,DE,
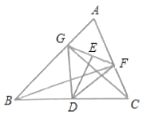
(1)求证:![]() 是等腰三角形.
是等腰三角形.
(2)若![]() ,求DE的长.
,求DE的长.
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a2b+c>0;④a+c>0,其中正确结论的个数为( )
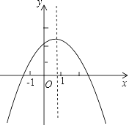
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
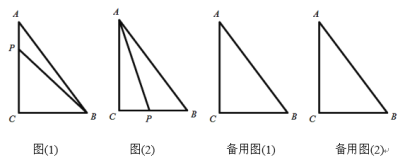
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点A开始沿着
,若动点P从点A开始沿着![]() 的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
(1)当![]() 时,
时,![]() 的面积是___________
的面积是___________![]() ;
;
(2)如图(2)当t为何值时,AP平分![]() ;
;
(3)当t为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:![]() >0.
>0.
解:设![]() =0,解得:
=0,解得:![]() =0,
=0,![]() =5,则抛物线y=
=5,则抛物线y=![]() 与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=
与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=![]() 的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即![]() >0,所以,一元二次不等式
>0,所以,一元二次不等式![]() >0的解集为:x<0或x>5.
>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式![]() <0的解集为 .
<0的解集为 .
(3)用类似的方法解一元二次不等式:![]() >0.
>0.
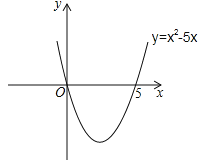
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为假命题的是( )
A.三条边分别对应相等的两个三角形全等B.三角形的一个外角大于与它相邻的内角
C.角平分线上的点到角两边的距离相等D.有一个角是![]() 的等腰三角形是等边三角形
的等腰三角形是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定 时,需付的行李费 y(元)是行李质量 x(千克)的一次函数,且部分对应关系如下表所示.

(1)求 y 关于 x 的函数关系式;
(2)求旅客最多可免费携带行李的质量;
(3)当行李费为 3≤y≤10 时,可携带行李的质量 x 的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com