
【题目】为了迎接元旦,孝昌县政府要在广场上设计一座三角形展台,要求园林工人把它的每条边上摆放上相等盆数的盆栽鲜花(如图所示的每个小圆圈表示一盆鲜花)以美化环境,如果每条边上摆放两盆鲜花,共需要3盆鲜花;如果每条边上摆放3盆鲜花,共需要6盆鲜花;…,按此要求摆放下去:

(1)根据图示填写下表:
每条边上摆放的盆数( | 2 | 3 | 4 | 5 | 6 | … |
共需要的盆数( | 3 | 6 | … |
(2)如果要在每条边上摆放![]() 盆鲜花,那么需要鲜花的总盆数 .
盆鲜花,那么需要鲜花的总盆数 .
(3)请你帮园林工人参考一下,能否用2020盆鲜花作出符合要求的摆放?如果能,请计算出每条边上应摆放花的盆数;如果不能,请说明理由.
【答案】(1)9,12,15;(2)S=3n-3 (n是大于2的整数);(3)不能
【解析】
(1)结合图形,发现:每条边上每增加一盆鲜花,总数就增加3盆,依此可得出答案.
(2)结合(1)中的规律即可求出每条边上摆n盆小菊花时需要小菊花的总盆数;
(3)根据题意把2020代入S=3(n-1)中,求出n的值后,即可作出判断.
解:(1)由图知,每条边上每增加一盆鲜花,总数就增加3盆,
故答案为:
每条边上摆放的盆数( | 2 | 3 | 4 | 5 | 6 | … |
共需要的盆数( | 3 | 6 | 9 | 12 | 15 | … |
(2)每条边摆两个,则总盆数=3=3(2-1),
每条边摆3个,则总盆数=6=3(3-1),
每条边摆4个,则总盆数=9=3(4-1),
…
每条边摆n个,则总盆数=3(n-1),
∴总盆数=3n-3 (n是大于2的整数)
(3)不能
∵(2020+3)÷3不是整数,
∴不能用2020盆鲜花作出符合要求的摆放.


科目:初中数学 来源: 题型:
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中五次行驶纪录如下。(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
-4 | +7 | -9 | +7 | -2 |
(1)求第二次记录时距A地多远?
(2)在第______次纪录时距A地最远。
(3)若每千米耗油0.8升,问共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
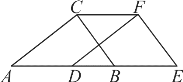
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=4cm,BC=3cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8cm,DB=2cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
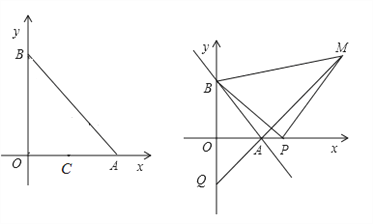
【题目】如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足![]()
(1)求A、B两点的坐标;
(2)C为OA的中点,作点C关于y轴的对称点D,以BD为直角边在第二象限作等腰Rt△BDE,过点E作EF⊥x轴于点F.若直线y=kx-4k将四边形OBEF分为面积相等的两部分,求k的值;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com