
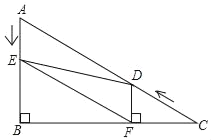
【题目】如图,在Rt△ABC中,∠B=90°,AC=12,∠A=60°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
【答案】(1)6;(2)EF与AD平行且相等,理由见解析;(3)t=4
【解析】
(1)在Rt△ABC中,∠C=30°,则AC=2AB,得到AB的值.
(2)先证四边形AEFD是平行四边形,从而证得AD∥EF,并且AD=EF,在运动过程中关系不变.
(3)求得四边形AEFD为平行四边形,若使AEFD为菱形则需要满足的条件及求得.
解:(1)Rt△ABC中,∠B=90°,∠A=60°.
∴∠C=30°
∵AC=12
∴AB=6,
故答案为:6;
(2)EF与AD平行且相等.
证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF,
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
∴四边形AEFD为平行四边形.
∴EF与AD平行且相等.
(3)能;理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又∵AE=DF,
∴四边形AEFD为平行四边形.
∵AB=6,AC=12.
∴AD=AC﹣DC=12﹣2t.
若使AEFD为菱形,则需AE=AD,
即t=12﹣2t,t=4.
即当t=4时,四边形AEFD为菱形.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
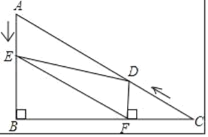
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
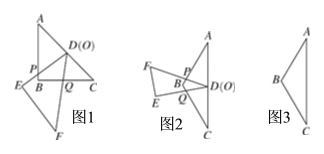
【题目】如图1,把两块全等的含45°角的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合.把三角板ABC固定不动,让三角板DEF绕点D旋转,两边分别与线段AB,BC相交于点P,Q,易说明△APD∽△CDQ.根据以上内容,回答下列问题:
(1)如图2,将含30°角的三角板DEF(其中∠EDF=30°)的锐角顶点D与等腰△ABC(其中∠ABC=120°)的底边中点O重合,两边DF,DE分别与边AB,BC相交于点P,Q.写出图中的相似三角形__ _ (直接填在横线上);
(2)其他条件不变,将三角板DEF旋转至两边DF,DE分别与边AB的延长线、边BC相交于点P,Q.上述结论还成立吗?请你在图3上补全图形,并说明理由;
(3)在(2)的条件下,连接PQ,△APD与△DPQ是否相似?请说明理由;
(4)根据(1)(2)的解答过程,你能否将两三角板改为更一般的三角形,使得(1)中的结论仍然成立?若能,请说明两个三角形应满足的条件;若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
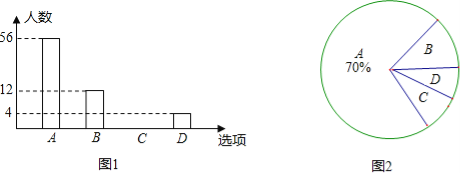
(1)本次调查共选取 名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
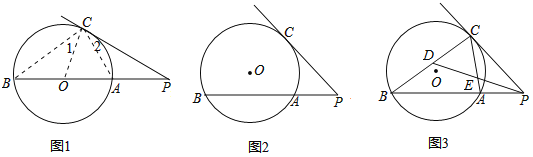
【题目】阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.
在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以![]() ,即PC2=PAPB.
,即PC2=PAPB.
问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC2=PAPB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
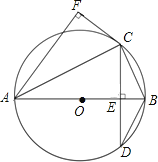
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在学校“青少年科技创新比赛”活动中,设计了一个沿直线轨道做匀速直线运动的模型.甲车从![]() 处出发向
处出发向![]() 处行驶,同时乙车从
处行驶,同时乙车从![]() 处出发向
处出发向![]() 处行驶.如图所示,线段
处行驶.如图所示,线段![]() 、
、![]() 分别表示甲车、乙车离
分别表示甲车、乙车离![]() 处的距离
处的距离![]() (米)与已用时间
(米)与已用时间![]() (分)之间的关系.试根据图象,解决以下问题:
(分)之间的关系.试根据图象,解决以下问题:
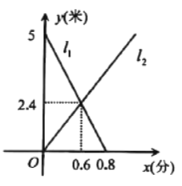
(1)填空:出发_________(分)后,甲车与乙车相遇,此时两车距离![]() 处________(米);
处________(米);
(2)求乙车行驶![]() (分)时与
(分)时与![]() 处的距离.
处的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家蓝莓采摘园的蓝莓品质相同,销售价格都是每千克30元,两家均推出了“周末”优惠方案.甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需要购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠.优惠期间,设某游客的蓝莓采摘量为![]() 千克,在甲采摘园所需总费用为
千克,在甲采摘园所需总费用为![]() 元,在乙采摘园所需总费用为
元,在乙采摘园所需总费用为![]() 元.
元.
(1)求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)该游客如何选择采摘园去采摘比较合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com