
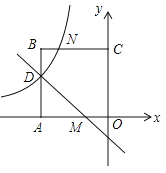
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
【答案】(1)![]() ,y=﹣x﹣1;(2)P为(﹣10,9)或(8,﹣9).
,y=﹣x﹣1;(2)P为(﹣10,9)或(8,﹣9).
【解析】
试题分析:(1)由正方形OABC的顶点C坐标,确定出边长,及四个角为直角,根据AD=2DB,求出AD的长,确定出D坐标,代入反比例解析式求出m的值,再由AM=2MO,确定出MO的长,即M坐标,将M与D坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)把y=3代入反比例解析式求出x的值,确定出N坐标,得到NC的长,设P(x,y),根据△OPM的面积与四边形OMNC的面积相等,求出y的值,进而得到x的值,确定出P坐标即可.
试题解析:(1)∵正方形OABC的顶点C(0,3),∴OA=AB=BC=OC=3,∠OAB=∠B=∠BCO=90°,∵AD=2DB,∴AD=![]() AB=2,∴D(﹣3,2),把D坐标代入
AB=2,∴D(﹣3,2),把D坐标代入![]() 得:m=﹣6,∴反比例解析式为
得:m=﹣6,∴反比例解析式为![]() ,∵AM=2MO,∴MO=
,∵AM=2MO,∴MO=![]() OA=1,即M(﹣1,0),把M与D坐标代入y=kx+b中得:
OA=1,即M(﹣1,0),把M与D坐标代入y=kx+b中得:![]() ,解得:k=b=﹣1,则直线DM解析式为y=﹣x﹣1;
,解得:k=b=﹣1,则直线DM解析式为y=﹣x﹣1;
(2)把y=3代入![]() 得:x=﹣2,∴N(﹣2,3),即NC=2,设P(x,y),∵△OPM的面积与四边形OMNC的面积相等,∴
得:x=﹣2,∴N(﹣2,3),即NC=2,设P(x,y),∵△OPM的面积与四边形OMNC的面积相等,∴![]() (OM+NC)OC=
(OM+NC)OC=![]() OM|y|,即|y|=9,解得:y=±9,当y=9时,x=﹣10,当y=﹣9时,x=8,则P坐标为(﹣10,9)或(8,﹣9).
OM|y|,即|y|=9,解得:y=±9,当y=9时,x=﹣10,当y=﹣9时,x=8,则P坐标为(﹣10,9)或(8,﹣9).


科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球5个,黄球2个,小明将球搅匀,从中任意摸出一个球.
(1)会有哪些可能的结果?
(2)若从中任意摸出一个球是白球的概率为0.5,求口袋中红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】口袋里有红、绿、黄三种颜色的球,除颜色外其余均相同,其中有红球4个,绿球3个,任意摸出一个球是绿球的概率是 ![]() .试求:
.试求:
(1)口袋里黄球的个数;
(2)任意摸出一个球是黄球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形①平行四边形;②菱形;③对角线互相垂直的四边形;④对角线相等的四边形,满足条件的是( )
A.①③④
B.②③
C.①②④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.
(1)证明:△AGE≌△ECF;
(2)求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组部分统计数据.
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数 | 23 | 31 | 60 | 127 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.254 | 0.253 |
|
(1)根据上表数据计算 ![]() = . 估计从袋中摸出一个球是黑球的概率是 . (精确到0. 01)
= . 估计从袋中摸出一个球是黑球的概率是 . (精确到0. 01)
(2)估算袋中白球的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com