
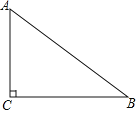
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的外心和内心之间的距离为_____.
【答案】![]()
【解析】
作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.先根据勾股定理求出AB=10,得到△ABC的外接圆半径AO=5,再证明四边形MECD是正方形,根据内心的性质和切线长定理,求出⊙M的半径r=2,则ON=1,然后在Rt△OMN中,运用勾股定理即可求解.
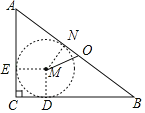
解:设△ABC的内切圆⊙M,O为△ACB的外接圆的圆心,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N,
在Rt△ABC中,∵∠ACB=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
∵点O为△ABC的外心,
∴AO为外接圆半径,AO=![]() AB=5,
AB=5,
设⊙M的半径为r,则MD=ME=r,
又∵∠MDC=∠MEC=∠C=90°,
∴四边形IECD是正方形,
∴CE=CD=r,AE=AN=6﹣r,BD=BN=8﹣r,
∵AB=10,
解得:r=2,
∴MN=r=2,AN=AE=6﹣r=6﹣2=4,
在Rt△OMN中,∵∠MNO=90°,ON=AO﹣AN=5﹣4=1,
∴OM=![]() ,
,
故答案为:![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2﹣4x+3
(1)求其图象与x轴交点A、B的坐标(A在B左边);
(2)在坐标系中画出函数图象;
(3)若函数图形的顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点M(0, ![]() )为圆心,以
)为圆心,以![]() 长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)求出CP所在直线的解析式;
(2)连接AC,请求△ACP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在改革开放30年纪念活动中,某校学生会就同学们对我国改革开放30年所取得的辉煌成就的了解程度进行了随机抽样调查,并将调查结果绘制成如图所示的统计图的一部分.
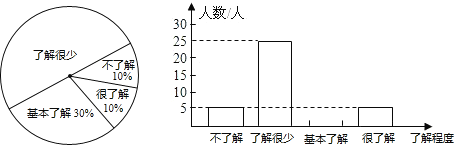
根据统计图中的信息,解答下列问题:
(1)本次抽样调查的样本容量是 .调查中“了解很少”的学生占 %;
(2)补全条形统计图;
(3)若全校共有学生1300人,那么该校约有多少名学生“很了解”我国改革开放30年来取得的辉煌成就.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD的中点,连接MN、NF.
问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为 ,线段MN和线段NF的数量关系为 ;
深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;
拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
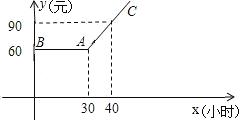
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com