
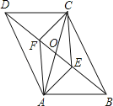
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
【答案】B.
【解析】
试题分析:∵DE=BF,
∴DF=BE,
在Rt△DCF和Rt△BAE中,
![]() ,
,
∴Rt△DCF≌Rt△BAE(HL),
∴FC=EA,(故①正确);
∵AE⊥BD于点E,CF⊥BD于点F,
∴AE∥FC,
∵FC=EA,
∴四边形CFAE是平行四边形,
∴EO=FO,(故②正确);
∵Rt△DCF≌Rt△BAE,
∴∠CDF=∠ABE,
∴CD∥AB,
∵CD=AB,
∴四边形ABCD是平行四边形,(故③正确);
由以上可得出:△CDF≌△BAE,△CDO≌△BAO,△CDE≌△BAF,
△CFO≌△AEO,△CEO≌△AFO,△ADF≌△CBE等.(故④错误).
故正确的有3个.
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
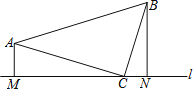
【题目】如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线![]() 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.
(1)求证:△AMC≌△CNB;
(2)若AM=3,BN=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,壁虎在一座底面半径为 2 米,高为 5 米的油罐的下底边沿点 A处,它 发现在自己的正上方油罐上边缘的点 B处有一只害虫,便决定捕捉这只害虫,为了不引起害 虫的注意,它故意不走直线,而是绕着油罐,沿一条螺旋路线,从背后对害虫进行突然袭击.结 果,壁虎偷袭成功,获得了一顿美餐.请问壁虎至少要爬行多少路程 才能捕到害虫?(π取 3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
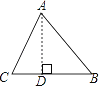
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=________;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
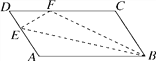
【题目】如图,在□ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为22,则□ABCD的周长为________,FC的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、 ![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)OA= cm,OB= cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com