

分析 根据两条直线平行,内错角相等,则∠BFE=∠DEF=18°,根据平角定义,则∠EFC=162°(图a),进一步求得∠BFC=162°-18°=144°(图b),进而求得∠CFE=144°-18°=126°(图c),依此类推,当角度小于19°时,就不能折叠了,即可求出折叠次数,注意折叠次数从图b是第一次折叠.
解答 解:∵AD∥BC,∠DEF=19°,
∴∠BFE=∠DEF=19°,
∴∠EFC=161°(图a),
∴∠BFC=161°-19°=142°(图b),(1次)
∴∠CFE=142°-19°=123°(图c). (2次)
依此类推:123°-19°=104° (3次)
104°-19°=85° (4次)
85°-19°=66° (5次)
66°-19°=47° (6次)
47°-19°=28° (7次)
28°-19°=9°. (8次)
故答案为:123°;8.
点评 此题主要考查了翻折变换的性质,根据折叠能够发现相等的角进而求出是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 目的地 车型 | A村(元/辆) | B村(元/辆) |
| 大货车 | 800 | 900 |
| 小货车 | 400 | 600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
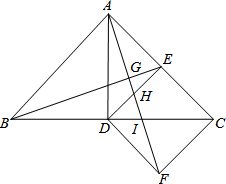 如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.
已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,P是等边三角形ABC内的一点,且PA=18,PB=24,PC=30.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为18,∠APB=150°.
如图所示,P是等边三角形ABC内的一点,且PA=18,PB=24,PC=30.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为18,∠APB=150°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.
如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA′处,求调整后点A′比调整前点A的高度降低了多少厘米(结果取整数)?
如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA′处,求调整后点A′比调整前点A的高度降低了多少厘米(结果取整数)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com