
科目:初中数学 来源: 题型:选择题
| A. | 审查一篇书稿有哪些科学性错误 | |
| B. | 了解你所在班级全体同学的视力情况 | |
| C. | 对乘坐飞机的旅客是否带违禁品的调查 | |
| D. | 了解某工厂生产出的一批轮胎的最大承受力 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
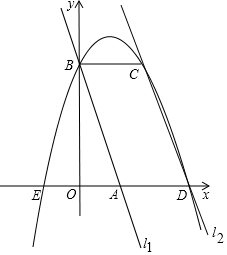 如图,在平面直角坐标系中2条直线为l1:y=-3x+3,l2:y=-3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
如图,在平面直角坐标系中2条直线为l1:y=-3x+3,l2:y=-3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.
已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
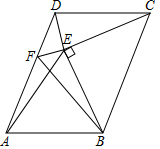 如图,在?ABCD中,以BC为斜边在?ABCD内作等腰直角△BCE,连接DE,过点E作EF⊥DE交AD于点F,∠CDE=∠CED=∠DCB.
如图,在?ABCD中,以BC为斜边在?ABCD内作等腰直角△BCE,连接DE,过点E作EF⊥DE交AD于点F,∠CDE=∠CED=∠DCB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com