
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2 ![]() ,则图中阴影部分面积是(结果保留π和根号)
,则图中阴影部分面积是(结果保留π和根号)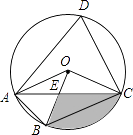
【答案】3π﹣2 ![]()
【解析】解:∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC﹣∠AOB=90°,
在Rt△OCE中,OC=2 ![]() ,
,
∴OE=OCtan∠OCE=2 ![]() tan30°=2
tan30°=2 ![]() ×
× ![]() =2,
=2,
∴S△OEC= ![]() OEOC=
OEOC= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() ,
,
∴S扇形OBC= ![]() =3π,
=3π,
∴S阴影=S扇形OBC﹣S△OEC=3π﹣2 ![]() .
.
所以答案是:3π﹣2 ![]() .
.
【考点精析】利用扇形面积计算公式对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
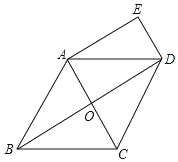
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若△ABC是边长为2的正三角形,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,![]() 的顶点都在格点上,建立平面直角坐标系,
的顶点都在格点上,建立平面直角坐标系,
(1)点A的坐标为______,点C的坐标为______;
(2)将![]() 先向右平移2个单位长度,再向下平移3个单位长度,请画出平移后的
先向右平移2个单位长度,再向下平移3个单位长度,请画出平移后的![]() ,并分别写出点A1、B1、C1的坐标;
,并分别写出点A1、B1、C1的坐标;
(3)求![]() 的面积.
的面积.
 0
0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:5
B.2:3
C.3:5
D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.

(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com