Question

14．如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm
（1）若OB=6cm．
①求点C的坐标；
②若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离；
（2）点C与点O的距离的最大值=12 cm．

Answer 1

分析 （1）①过点C作y轴的垂线，垂足为D，利用含30°角的直角三角形的性质解答即可；
②设点A向右滑动的距离为x，得点B向上滑动的距离也为x，利用三角函数和勾股定理进行解答；
（2）过C作CE⊥x轴，CD⊥y轴，垂足分别为E，D，证明△ACE与△BCD相似，再利用相似三角形的性质解答．

解答 解：（1）①过点C作y轴的垂线，垂足为D，如图1：

在Rt△AOB中，AB=12，OB=6，则BC=6，
∴∠BAO=30°，∠ABO=60°，
又∵∠CBA=60°，
∴∠CBD=60°，∠BCD=30°，
∴BD=3，CD=3$\sqrt{3}$，
所以点C的坐标为（-3$\sqrt{3}$，9）；
②设点A向右滑动的距离为x，根据题意得点B向上滑动的距离也为x，如图2：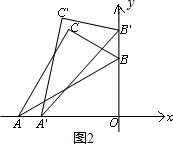

AO=12×cos∠BAO=12×cos30°=6$\sqrt{3}$．
∴A'O=6$\sqrt{3}$-x，B'O=6+x，A'B'=AB=12
在△A'O B'中，由勾股定理得，
（6$\sqrt{3}$-x）²+（6+x）²=12²，
解得：x=6（$\sqrt{3}$-1），
∴滑动的距离为6（$\sqrt{3}$-1）；
（2）设点C的坐标为（x，y），过C作CE⊥x轴，CD⊥y轴，垂足分别为E，D，如图3：

则OE=-x，OD=y，
∵∠ACE+∠BCE=90°，∠DCB+∠BCE=90°，
∴∠ACE=∠DCB，
又∵∠AEC=∠BDC=90°，
∴△ACE∽△BCD，
∴$\frac{CE}{CD}=\frac{AC}{BC}$，即$\frac{CE}{CD}=\frac{6\sqrt{3}}{6}=\sqrt{3}$，
∴y=-$\sqrt{3}$x，
OC²=x²+y²=x²+（-$\sqrt{3}$x）²=4x²，
∴取AB中点D，连接CD，OD，则CD与OD之和大于或等于CO，当且仅当C，D，O三点共线时取等号，此时CO=CD+OD=6+6=12，
故答案为：12．
第二问方法二：因角C与角O和为180度，所以角CAO与角CBO和为180度，故A，O，B，C四点共圆，且AB为圆的直径，故弦CO的最大值为12．

点评 此题考查相似三角形的综合题，关键是根据相似三角形的性质和勾股定理以及三角函数进行分析解答．