
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

【答案】(1)![]() 秒后△PCQ的面积为3平方厘米,此时PQ的长是
秒后△PCQ的面积为3平方厘米,此时PQ的长是![]() ;
;
(2)经过![]() 秒或
秒或![]() 秒,以A、B、P、Q为顶点的四边形的面积为22cm2
秒,以A、B、P、Q为顶点的四边形的面积为22cm2
【解析】试题分析:(1)根据题意∠C=90°,可以得出△PCQ的面积为![]() ×PC×CQ,设出t秒后满足要求,则根据△PCQ的面积是3 cm2列出等量关系求出t的值即可.
×PC×CQ,设出t秒后满足要求,则根据△PCQ的面积是3 cm2列出等量关系求出t的值即可.
(2)根据四边形ABQP的面积=SΔABC-SΔPCQ,列式计算即可.
试题解析:(1)设t秒后△PCQ的面积为3平方厘米,
则有PC=t cm,CQ=3t cm,
依题意,得: ![]() t×3t=3,
t×3t=3,
![]()
![]() (舍去)
(舍去)
由勾股定理,得:PQ=![]()
答: ![]() 秒后△PCQ的面积为3平方厘米,此时PQ的长是
秒后△PCQ的面积为3平方厘米,此时PQ的长是![]()
(2)① 当P在线段AC上,Q在线段BC上时, ![]()
S四边形APQB= S△ABC﹣S△PQC
![]()
![]() ,
,
得![]() (舍去)
(舍去)
② 当P在线段AC上,Q在线段BC延长线上时, ![]()
S四边形APBQ= S△AQC﹣S△PBC=![]()
![]() ,得
,得![]()
③ 当P在线段AC的延长线上,Q在线段BC延长线上时, ![]()
S四边形ABQP= S△PQC﹣S△ABC=![]()
![]() (不符合题意,舍去),(或者得
(不符合题意,舍去),(或者得![]() ,
, ![]() ,都不符合题意,舍去)
,都不符合题意,舍去)
综上: ![]() 或
或![]()
答,经过![]() 秒或
秒或![]() 秒,以A、B、P、Q为顶点的四边形的面积为22cm2
秒,以A、B、P、Q为顶点的四边形的面积为22cm2


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示. 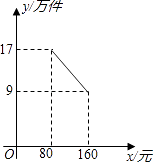
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区在实施居民用水管理前,随机调查了部分家庭(单位:户)去年的月均用水量(单位:t),并将调查数据进行整理,绘制出如下不完整的统计图表:

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区有2000户家庭,根据此次随机抽查的数据估计,该小区月均用水量不低于20t的家庭有多少户?
(3)为了鼓励节约用水,要确定一个月均用水量的标准,超出该标准的部分按1.5倍价格收费,若要使68%的家庭水费支出不受影响,那么,你觉得家庭月均用水量应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
(1)y的值随x值的增大而 (填“增大”或“减小”);
(2)图象与x轴的交点坐标是 ;图象与y轴的交点坐标是 ;
(3)当x 时,y <0 ;
(4)直线y=-2x+3与两坐标轴所围成的三角形的面积是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,BE平分
,BE平分![]() ,
,![]() .
.
![]() 与BC平行吗?请说明理由;
与BC平行吗?请说明理由;
![]() 与EF的位置关系如何?为什么?
与EF的位置关系如何?为什么?
解:![]() 理由如下:
理由如下:
![]() 平角的定义
平角的定义![]()
![]() 已知
已知![]()
![]() ______
______![]() ______
______![]()
![]() ______
______
![]() 与EF的位置关系是______
与EF的位置关系是______
![]() 平分
平分![]() 已知
已知![]()
![]() 角平分线的定义
角平分线的定义![]()
又![]() ,
,![]() 已知
已知![]() 即
即![]()
![]() ______
______![]() 等量代换
等量代换![]()
![]() ______
______![]() ______
______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
![]() 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元?
![]() 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1 , 0),C(x2 , 0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当0<t≤8时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
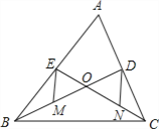
【题目】如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2![]() ,OD+CD=7,求△OCB的面积.
,OD+CD=7,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() 所示,在
所示,在![]() 中,
中,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() 的周长
的周长![]() ;21.
;21.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,试判断
,试判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
![]() 如图
如图![]() 所示,在
所示,在![]() 中,若
中,若![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com