
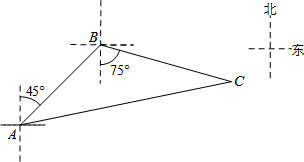
 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度. 分析 设捕鱼船的速度为x海里/小时,由题意得出:∠ABC=45°+75°=120°,AB=12,BC=2x,AC=14×2=28,过点A作AD⊥CB的延长线于点D,在Rt△ABD中,由三角函数得出BD、AD的长度,得出CD=2x+6.在Rt△ACD中,由勾股定理得出方程,解方程即可.
解答 解: 设捕鱼船的速度为x海里/小时;如图所示,
设捕鱼船的速度为x海里/小时;如图所示,
由题意得:∠ABC=45°+75°=120°,AB=12,BC=2x,AC=14×2=28,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°-75°)=60°,
∴BD=AB•cos60°=$\frac{1}{2}$AB=6,AD=AB•sin60°=6$\sqrt{3}$,
∴CD=2x+6.
在Rt△ACD中,由勾股定理得:282=(6$\sqrt{3}$)2+(2x+6)2,
解得:x=16,(负值舍去),
答:捕鱼船的速度为16海里/小时.
点评 本题考查了解直角三角形的应用、勾股定理、三角函数;由三角函数和勾股定理得出方程是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1尾 | B. | 50尾 | C. | 500尾 | D. | 1 000尾 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
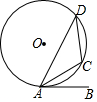 如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.
如图,$\widehat{AC}$=$\widehat{DC}$,AC平分∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
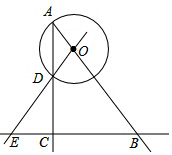 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | n |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.
如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
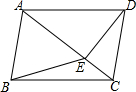 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com