
 如图,正六边形的面积为120,P是其内任意一点,求三角形PBC和三角形PEF的面积之和是多少?
如图,正六边形的面积为120,P是其内任意一点,求三角形PBC和三角形PEF的面积之和是多少? 分析 假设P到BC 的距离为h1,P到EF 的距离为h2,BC到EF的距离为h,则h1+h2=h.再假设正六边形边长为a,中心到各边的距离为d,则h=2d;然后利用面积公式可得出△PBC的面积+△PEF的面积和,再与正六边形比较,得出正六边形的面积是△PBC的面积+△PEF的面积和的三倍,从而得出答案.
解答 解:假设P到BC 的距离为h1,P到EF 的距离为h2,BC到EF的距离为h,则h1+h2=h.再假设正六边形边长为a,中心到各边的距离为d,则h=2d;
△PBC的面积+△PEF的面积
=a×h1÷2+a×h2÷2
=a×(h1+h2)÷2
=a×h÷2
=a×2d÷2
=ad,
正六边形的面积=(a×d÷2)×6
=3ad,
所以正六边形的面积=3(△PBC的面积+△PEF的面积)
所以△PBC的面积+△PEF的面积=$\frac{120}{3}$=40.
答:△PBC的面积和△PEF的面积之和为40.
点评 本题考查正六边形的性质,三角形的面积等知识,解答此题的关键是得出正六边形的面积是△PBC的面积+△PEF的面积和的三倍.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
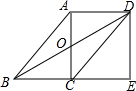 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,延长BC到点E,使得BC=CE,连结DE.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,延长BC到点E,使得BC=CE,连结DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -$\frac{3}{2}$ | D. | $-\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,直线l1∥l2,点∠α、∠β夹在两平行线之间.
如图所示,直线l1∥l2,点∠α、∠β夹在两平行线之间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com