
【题目】近期猪肉价格不断走高,引起市民与政府的高度关注,当市场猪肉的平均价格达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%,某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉,并规定其销售价格在5月20日每千克40元的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了![]() ,求a的值.
,求a的值.
科目:初中数学 来源: 题型:
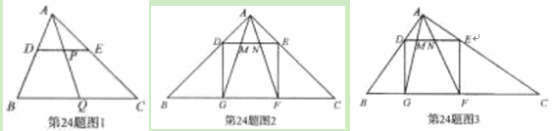
【题目】(本题满分10分)(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:![]() .
.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证MN2=DM·EN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
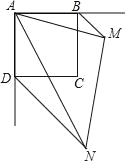
【题目】已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
(1)求证:△ABM∽△NDA;
(2)联结BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC的内角平分线与外角平分线分别交BC及BC的延长线于点P、Q.
(1)求∠PAQ的大小;
(2)若点M为PQ的中点,求证:PM2=CM·BM.
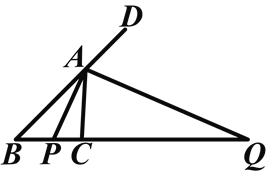
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张矩形纸片ABCD,![]() ,
,![]() .
.
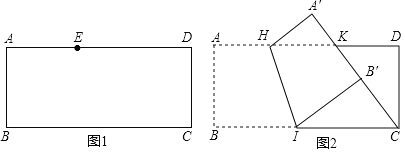
![]() 如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为
如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为![]() 点M,N分别在边AD,BC上
点M,N分别在边AD,BC上![]() ,利用直尺和圆规画出折痕
,利用直尺和圆规画出折痕![]() 不写作法,保留作图痕迹
不写作法,保留作图痕迹![]() ;
;
![]() 如图2,点K在这张矩形纸片的边AD上,
如图2,点K在这张矩形纸片的边AD上,![]() ,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点
,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点![]() ,
,![]() 处,小明认为
处,小明认为![]() 所在直线恰好经过点D,他的判断是否正确,请说明理由.
所在直线恰好经过点D,他的判断是否正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
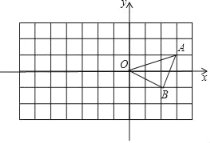
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示,解答问题:
(1)请按要求对△OAB作变换:以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA′B′.
(2)写出点A′的坐标;
(3)求△OA′B'的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() ,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移
,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移![]() 个单位长度后,与x轴交于点A、B,
个单位长度后,与x轴交于点A、B,![]() 在B的左侧
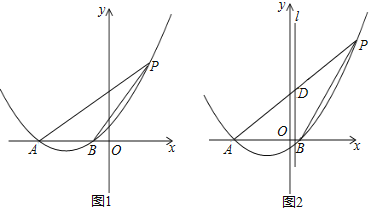
在B的左侧![]() ,如图1,P为平移后的抛物线上位于第一象限内的一点
,如图1,P为平移后的抛物线上位于第一象限内的一点
![]() 点A的坐标为______;
点A的坐标为______;
![]() 若点P的横坐标为
若点P的横坐标为![]() ,求出当m为何值时
,求出当m为何值时![]() 的面积最大,并求出这个最大值;
的面积最大,并求出这个最大值;
![]() 如图2,AP交l于点D,当D为AP的中点时,求证:
如图2,AP交l于点D,当D为AP的中点时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com