
【题目】某房间窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同):
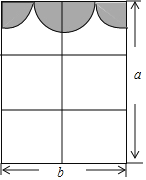
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光的部分的面积是多少?
(3)计算当a=6,b=4时,窗户中能射进阳光的部分的面积.(π取3.14)
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于( )

A. 1 B. 1.5 C. 2 D. 0.8或1.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡水蜜桃享誉海内外,老王用3000元购进了一批水蜜桃.第一天,很快以比进价高40% 的价格卖出150千克.第二天,他发现剩余的水蜜桃卖相已不太好,于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出,本次生意老王一共获利750元.
(1)根据以上信息,请你编制一个问题,并给予解答;
(2)老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克,第二天,老王把卖相不好的水蜜桃挑出,单独打折销售,售价为10元/千克,结果很快被一抢而空,其余的仍按第一天的价格销售,且当天全部售完.若老王这次至少获利1100元,请问打折销售的水蜜桃最多多少千克?(精确到1千克.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
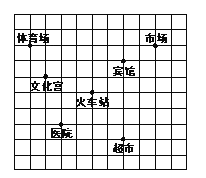
(1)请你以火车站为原点建立平面直角坐标系;
(2)写出市场、超市的坐标;
(3)请将体育场、宾馆和火车站看作三点用线段连起来,得![]() ,然后将此三角形向下平移4个单位长度,再画出平移后的
,然后将此三角形向下平移4个单位长度,再画出平移后的![]() ;
;
(4)根据坐标情况,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在电器进入销售旺季,福清某电器超市销售每台进价分别为![]() 元、
元、![]() 元的
元的![]() 两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 两种型号的电器销售单价;
两种型号的电器销售单价;
(2)若超市准备用不超过![]() 元的金额再采购这种型号的电器共
元的金额再采购这种型号的电器共![]() 台,销售完这
台,销售完这![]() 台电器实现利润超过
台电器实现利润超过![]() 元的目标,请给出相应的采购方案;并求出利润的最大值.
元的目标,请给出相应的采购方案;并求出利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数 1,3,5,7,9,…,排成如图的数阵.
(1)十字框中的五个数的和与中间数 15 有什么关系?
(2)设中间数为 a,用式子表示十字框中五个数之和;
(3)十字框中五个数之和能等于 2 005 吗?若能,请写出这五个数;若不能, 说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com