
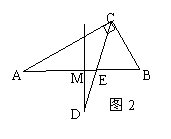
 16、In Fig.,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=
16、In Fig.,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=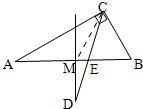 解:连接CM.
解:连接CM.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
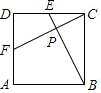 Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is
Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is查看答案和解析>>
科目:初中数学 来源: 题型:
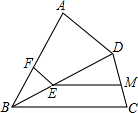 In fig 1,ABCD is a quadrilsteral,E is a point the diagonal BD,EF∥AD,EM∥BC,then the value of
In fig 1,ABCD is a quadrilsteral,E is a point the diagonal BD,EF∥AD,EM∥BC,then the value of | EF |
| DA |
| EM |
| BC |
| EF |
| DA |
| EM |
| BC |
| A、greater than 1(大于1) |
| B、equal to 1(等于1) |
| C、less than 1(小于1) |
| D、variable depending on the position of E(不能确定,与E的位置有关) |
查看答案和解析>>
科目:初中数学 来源: 题型:
In Fig.2,In the Rt△ABC,∠ACB=900,∠A=300,CD is the bisector to
∠ACB,MD is the perpendicular to BA and MD through the midpoint of segme![]() nt AB,thrn ∠CDM= .(英语小词典:bisector:平分线;perpendicular:垂线;midpoint:中点)
nt AB,thrn ∠CDM= .(英语小词典:bisector:平分线;perpendicular:垂线;midpoint:中点)
查看答案和解析>>
科目:初中数学 来源: 题型:
Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively ,BE and CF intersect at a point P.Then the length of line segment CP is __________.
(英汉词典:figure(缩写Fig.)图;length 长度;square 正方形;mid-point中点;intersect 相交;line segment 线段)
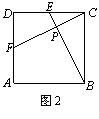
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com