练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．一个几何体的三视图如图所示，则这个几何体的侧面积是（　　）
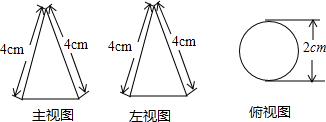
    A．4πB．2πC．4D．π

    分析 首先判断该几何体的形状，然后根据其尺寸求得其侧面积即可．

    解答 解：观察三视图发现该几何体为圆锥，其底面直径为2cm，母线长为4cm，
    所以其侧面积为：$\frac{1}{2}$×2π×4=4π，
    故选A．

    点评 本题考查了由三视图判断几何体，圆锥的有关计算，由该三视图中的数据确定圆锥的底面直径和母线长是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年贵州省七年级下学期第一次月考数学试卷（解析版） 题型：单选题

    某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（ ）

    A. 第一次左拐30°，第二次右拐30°

    B. 第一次右拐50°，第二次左拐130°

    C. 第一次右拐50°，第二次右拐130°

    D. 第一次向左拐50°，第二次向左拐120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在正方形ABCD中，点P在射线AB上，连结PC，PD，M，N分别为AB，PC中点，连结MN交PD于点Q．
    （1）如图1，当点P与点B重合时，求∠QMB的度数；
    （2）当点P在线段AB的延长线上时．
    ①依题意补全图2
    ②小聪通过观察、实验、提出猜想：在点P运动过程中，始终有QP=QM．
    小聪把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
    想法1延长BA到点E，使AE=PB．要证QP=QM，只需证△PDA≌△ECB．
    想法2：取PD中点E，连结NE，EA．要证QP=QM只需证四边形NEAM是平行四边形．
    想 法3：过N作NE∥CB交PB于点E，要证QP=QM，只要证明△NEM∽△DAP．
    …
    请你参考上面的想法，帮助小聪证明QP=QM．（一种方法即可）

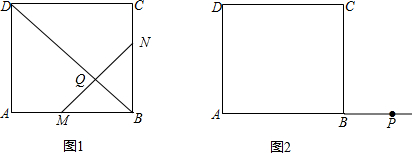
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

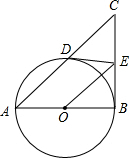    9．如图，AB为⊙O的直径，E是⊙O外一点，过点E作⊙O的两条切线ED、EB，切点分别为点D，B，连接AD并延长交BE延长线于点C，连接OE．
    （1）试判断OE与AC的关系，并说明理由；
    （2）填空：
    ①当∠BAC=45°时，四边形ODEB是正方形．
    ②当∠BAC=30°时，$\frac{AD}{DE}$的值为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

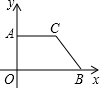    16．如图，在平面直角坐标系xOy中，点A、B的坐标分别为（0，3）、（7，0），点C在第一象限，AC∥x轴，∠OBC=45°．
    （1）求点C的坐标；
    （2）点D在线段AC上，CD=1，点E的坐标为（n，0），在直线DE的右侧作∠DEG=45°，直线EG与直线BC相交于点F，设BF=m，当n＜7且n≠0时，求m关于n的函数解析式，并直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放，若∠1=58°，则∠2的度数为（　　）
    A．30°B．32°C．42°D．58°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．解不等式组：$\left\{\begin{array}{l}{2x≤3（x+2）-5①}\\{\frac{1-2x}{4}+\frac{1}{5}＜0②}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

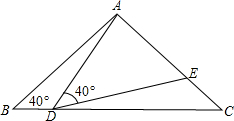    10．如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
    （1）点D从B向C运动时，∠BDA逐渐变小（填“大”或“小”）；设∠BAD=x°，∠BDA=y°，求y与x的函数关系式；
    （2）当DC的长度是多少时，△ABD≌△DCE，请说明理由；
    （3）在点D的运动过程中，△ADE的形状也在改变，当∠BDA等于多少度时，△ADE是等腰三角形？判断并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）$\root{3}{\frac{1}{8}}$+$\sqrt{（-3）^{2}}$-$\frac{5}{2}$$\root{3}{-\frac{1}{125}}$
    （2）|$\sqrt{3}$-$\sqrt{2}$|+|$\sqrt{3}$-2|-|$\sqrt{2}$-1|

    查看答案和解析>>

    同步练习册答案