
��ͼ��������6��1����15�յĿ�������ָ����������ͳ��ͼ����������ָ��С��100��ʾ����������������������ָ������200��ʾ���������ض���Ⱦ��ij�����ѡ��6��1����6��14���е�ijһ�쵽����������ͣ��2�죮
��1������˵��ﵱ���������������������
��2�������������ͣ��2���ڼ�ֻ��һ������������ض���Ⱦ�ĸ��ʣ�
��3��������ͳ��ͼ�жϴ����쿪ʼ��������Ŀ�������ָ���������ֻд���ۣ���
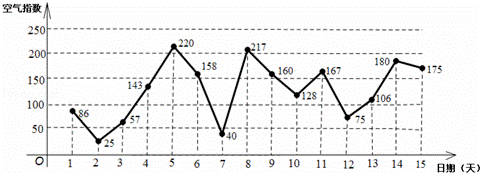


�⣺��1�����˵��ﵱ����������������У���1�졢��2�졢��3�졢��7�졢��12�죬��5�죻
��2��������������ͣ������Ŀ�������ָ���ǣ���86��25������25��57������57��143������143��220������220��158������158��40����
��40��217������217��160������160��128������128��167������167��75������75��106������106��180������180��175����
��14��ͣ��ʱ��Σ��ڼ�ֻ��һ����������ض���Ⱦ���У���4�쵽����5�쵽����7�쵽����8�쵽��
��ˣ�P��������ͣ���ڼ�ֻ��һ����������ض���Ⱦ��=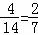 ��
��

 ��3����������ͼ�ɵôӵ�5�쿪ʼ�ĵ�5�졢��6�졢��7����������Ŀ�������ָ���������
��3����������ͼ�ɵôӵ�5�쿪ʼ�ĵ�5�졢��6�졢��7����������Ŀ�������ָ���������


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ������ABC����ÿ��С�����εı߳�Ϊ1�������У���A��B��C�����ڸ���ϣ���һ��Բ��ȥ���ǡ�ABC���ܹ���ȫ������������ε���СԲ��İ뾶��������



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��Rt��ABC�У���C=90�㣬P��BC���ϲ�ͬ��B��C��һ���㣬��P��PQ��AB������ΪQ������AP��
��1����˵�����۵�P��BC���Ϻδ�ʱ�����С�PBQ���ABC���ƣ�
��2����AC=3��BC=4����BPΪ��ֵʱ����AQP������������ֵ��
��3����Rt��ABC�У�����ֱ�DZ�BC��AC�����ϵʽBC=��AC���Ƿ����һ���˵�ֵ��ʹRt��AQP����Rt��ACPȫ�ȣ�Ҳ��Rt��BQPȫ�ȣ�
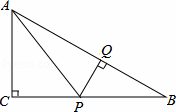


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��Ҫ����B�㵽�Ӱ�AD�ľ��룬��A���á�BAD=30�㣬��C���á�BCD=60�㣬�ֲ��AC=100�ף���B�㵽�Ӱ�AD�ľ���Ϊ��������
�� A�� 100�� B�� 50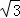 �� C��
�� C�� 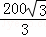 �� D�� 50��
�� D�� 50��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
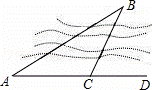
��֪����ƽ����l1��l2֮��ľ���Ϊ6������CD�ֱ�l1��l2��C��D���㣬һֱ�ǵĶ���P���߶�CD���˶�����P�����C��D�غϣ���ֱ�ǵ����߷ֱ�l1��l2��A��B���㣮
��1����������
��ͼ1������P��ֱ��l3��l1����PE��l1����E�Ǵ��㣬����B��BF��l3����F�Ǵ��㣮��ʱ��С����Ϊ��PEA�ס�PFB����ͬ����Ϊʲô��
��2��������֤
��ֱ�ǡ�APB��ͼ1��λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������һ�����У��Թ۲졢���룺��AE����ʲô����ʱ���Ե�P��A��BΪ������������ǵ��������Σ���ͼ2�л���ͼ�Σ�֤����IJ��룮
��3������̽��
�ڣ�2���������£�������CD��ֱ��l1���еĶ۽�Ϊ150��ʱ����CP=x����̽�����Ƿ����ʵ��x��ʹ��PAB�ı�AB�ij�Ϊ4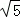 ����˵�����ɣ�
����˵�����ɣ�
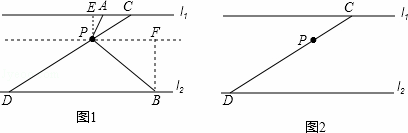


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com