
【题目】如图,笑笑和爸爸想要测量直立在地面上的建筑物OP与广告牌AB的高度.首先,笑笑站在离广告牌B处4米的D处看到广告牌AB的顶端A、建筑物OP的顶端O一条直线上;此时,在阳光下,爸爸站在N处,他的影长NE=2.1米,同一时刻,测得建筑物OP的影长为PG=28米,已知建筑物OP与广告牌AB之间的水平距离为11米,笑笑的眼睛到地面的距离CD=1.5米,爸爸的身高MN=1.8米.
(1)请你画出表示建筑物OP在阳光下的影子PG;
(2)求:①建筑物OP的高度;
②广告牌AB的高度.
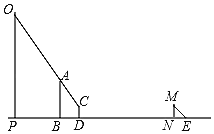
【答案】(1)见解析,(2)①24;②7.5
【解析】
(1)根据同一时刻光线平行过点O作ME的平行线交PE于点G即可画出建筑物OP在阳光下的影子PG;
(2)①由△OPG∽△MNE,得物高比物高等于影长比影长列比例式求解即可;
②作CF⊥OP于点F,交AB于点H,证△OFC∽△AHC,得对应边成比例即可求得AB的长.
解:(1)如图:PG即为建筑物OP在阳光下的影子.
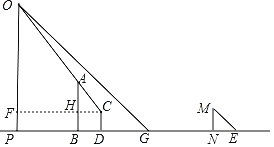
(2)①根据题意,得OP∥MN,OG∥ME,
∴∠OPG=∠MNE,∠OGP=∠MEN,
∴△OPG∽△MNE,
∴![]() ,即
,即![]() ,
,
解得OP=24.
答:建筑物OP的高度为24m.
②过点C作CF⊥OP于点F,交AB于点H,
则∠OFC=∠AHC=90°,∠OCF=∠ACH,
FH=PB=11,HC=BD=4,CD=HB=FP=1.5,
则OF=OP﹣PF=24﹣1.5=22.5,FC=PD=PB+BD=15.
∴△OFC∽△AHC,
∴![]() ,即
,即![]() ,
,
解得AH=6.
∴AB=AH+BH=6+1.5=7.5.
答:广告牌AB的高度为7.5m.


科目:初中数学 来源: 题型:
【题目】定义:如图![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在抛物线上(点
在抛物线上(点![]() 与
与![]() 两点不重合),如果
两点不重合),如果![]() 的三边满足
的三边满足![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() 的勾股点。
的勾股点。
(![]() )直接写出抛物线
)直接写出抛物线![]() 的勾股点的坐标;
的勾股点的坐标;
(![]() )如图
)如图![]() ,已知抛物线
,已知抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 的勾股点,求抛物线
的勾股点,求抛物线![]() 的函数表达式;
的函数表达式;
(![]() )在(
)在(![]() )的条件下,点
)的条件下,点![]() 在抛物线
在抛物线![]() 上,求满足条件
上,求满足条件![]() 的点
的点![]() (异于点
(异于点![]() )的坐标.
)的坐标.
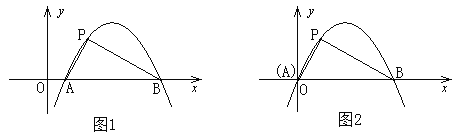
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字![]() ,2,3且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为
,2,3且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为![]() 的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为
的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为![]() 的值,两次结果记为
的值,两次结果记为![]() .
.
(1)请你帮他们用画树状图或列表的方法表示![]() 所有可能出现的结果;
所有可能出现的结果;
(2)若将记录结果![]() 看成平面直角坐标系中的一点,求
看成平面直角坐标系中的一点,求![]() 是第一象限内的点的概率.
是第一象限内的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一节数学课后,老师布置了一道课后练习题:
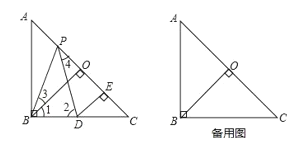
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
理清思路,本题证明的思路可用下列框图表示:
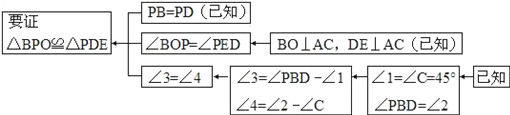
根据上述思路,请你完成下列问题.
(1)若BP平分∠ABO,其余条件不变.求证:AP=CD.
(2)若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系,并证明得出的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点M在BC边上,且BM=![]() BC,AM与BD相交于点N,那么S△BMN:S平行四边形ABCD为( )
BC,AM与BD相交于点N,那么S△BMN:S平行四边形ABCD为( )

A.1:3B.1:9C.1:12D.1:24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月5日是学雷锋日,也是中国青年志愿者服务日.今年3月5日,某中学组织全体学生参加了“青年志愿者”活动,活动分为“打扫街道(记为A)”“去敬老院服务(记为B)”“到社区文艺演出(记为C)”三项.
(1)八年级计划在3月5日这天随机完成“青年志愿者”活动中的一项,求八年级完成的恰好是“去敬老院服务”的概率;
(2)九年级计划在3月5日这天随机完成“青年志愿者”活动中的两项,请用列表或画树状图法求九年级完成的恰好是“打扫街道”和“去敬老院服务”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
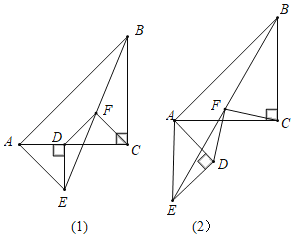
【题目】已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF,CF.
(1)如图1,点D在AC上,请你判断此时线段DF,CF的关系,并证明你的判断;
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45度时,若AD=DE=2,AB=6,求此时线段CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com