
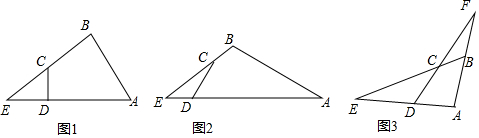
分析 (1)只要证明△EDC∽△EBA,可得$\frac{ED}{EB}$=$\frac{EC}{EA}$,即可证明ED•EA=EC•EB;
(2)如图2中,过C作CF⊥AD于F,AG⊥EB于G.想办法求出EB,AG即可求出△ABE的面积,即可解决问题;
(3)如图3中,作CH⊥AD于H,则CH=4,DH=3,作AG⊥DF于点G,设AD=5a,则DG=3a,AG=4a,只要证明△AFG∽△CEH,可得$\frac{AG}{CH}$=$\frac{FG}{EH}$,即$\frac{4a}{5+n-3a}$=$\frac{4}{n+3}$,求出a即可解决问题;
解答 解:(1)如图1中,
∵∠ADC=90°,∠EDC+∠ADC=180°,
∴∠EDC=90°,
∵∠ABC=90°,
∴∠EDC=∠ABC,
∵∠E=∠E,
∴△EDC∽△EBA,
∴$\frac{ED}{EB}$=$\frac{EC}{EA}$,
∴ED•EA=EC•EB.
(2)如图2中,过C作CF⊥AD于F,AG⊥EB于G.
在Rt△CDF中,cos∠ADC=$\frac{3}{5}$,
∴$\frac{DF}{CD}$=$\frac{3}{5}$,∵CD=5,
∴DF=3,
∴CF=$\sqrt{C{D}^{2}-D{F}^{2}}$=4,
∵S△CDE=6,
∴$\frac{1}{2}$•ED•CF=6,
∴ED=$\frac{12}{CF}$=3,EF=ED+DF=6,
∵∠ABC=120°,∠G=90°,∠G+∠BAG=∠ABC,
∴∠BAG=30°,
∴在Rt△ABG中,BG=$\frac{1}{2}$AB=6,AG=$\sqrt{A{B}^{2}-B{G}^{2}}$=6$\sqrt{3}$,
∵CF⊥AD,AG⊥EB,
∴∠EFC=∠G=90°,∵∠E=∠E,
∴△EFC∽△EGA,
∴$\frac{EF}{EG}$=$\frac{CF}{AG}$,
∴$\frac{6}{EG}$=$\frac{4}{6\sqrt{3}}$,
∴EG=9$\sqrt{3}$,
∴BE=EG-BG=9$\sqrt{3}$-6,
∴S四边形ABCD=S△ABE-S△CDE=$\frac{1}{2}$(9$\sqrt{3}$-6)×6$\sqrt{3}$-6=75-18$\sqrt{3}$.
(3)如图3中,作CH⊥AD于H,则CH=4,DH=3,
∴tan∠E=$\frac{4}{n+3}$,
作AG⊥DF于点G,设AD=5a,则DG=3a,AG=4a,
∴FG=DF-DG=5+n-3a,
∵CH⊥AD,AG⊥DF,∠E=∠F,
易证△AFG∽△CEH,
∴$\frac{AG}{CH}$=$\frac{FG}{EH}$,
∴$\frac{4a}{5+n-3a}$=$\frac{4}{n+3}$,
∴a=$\frac{n+5}{n+6}$,
∴AD=5a=$\frac{5(n+5)}{n+6}$.
点评 本题考查相似形综合题、相似三角形的判定和性质、直角三角形的30度角性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
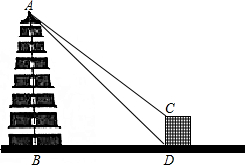 “大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年,玄樊为藏经典而修建,塔身七层,被视为古都西安的象征.民间人士道:“不到大雁塔,不算到西安”.小明在学习了锐角三角函数后,想用所学知识测量“大雁塔”的高度,小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“大雁塔”的高AB的长度.(结果精确到0.1米)(参考数据:sin37.5°≈0.6088,cos37.5°≈0.7934,tan37.5°≈0.7673.
“大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年,玄樊为藏经典而修建,塔身七层,被视为古都西安的象征.民间人士道:“不到大雁塔,不算到西安”.小明在学习了锐角三角函数后,想用所学知识测量“大雁塔”的高度,小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“大雁塔”的高AB的长度.(结果精确到0.1米)(参考数据:sin37.5°≈0.6088,cos37.5°≈0.7934,tan37.5°≈0.7673.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠A>∠B.
如图,在△ABC中,∠A>∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
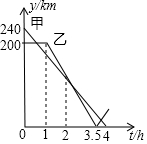 在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地.在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2$\frac{5}{7}$h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是②③④(填写所有正确结论的序号).
在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地.在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2$\frac{5}{7}$h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是②③④(填写所有正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.
今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.| 等级 | 得分x(分) | 频数(人) |
| A | 95≤x≤100 | 4 |
| B | 90≤x<95 | m |
| C | 85≤x<90 | n |
| D | 80≤x<85 | 24 |
| E | 75≤x<80 | 8 |
| F | 70≤x<75 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com