
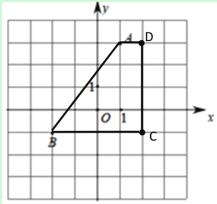
【题目】(1)如图1所示,写出A、B的坐标:A_________、B________;
(2)如图1所示,将点A向右平移1个单位到点D,点C、B关于y轴对称,求出四边形ABCD的面积;
(3)将图1中的网格去掉得到图2所示,直线AB的交y轴于点C,直线CD⊥AB于点C,△ACD为等腰直角三角形,且∠ACD=90°,求点D的坐标.


【答案】(1)(1,3);(-2,-1);(2)10;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由平面直角坐标易写出A、B坐标;
(2)利用两坐标平移和对称的特点找出C、D的位置,再求四边形ABCD的面积即可.
(3)图中没有说明点D的位置,故需分类讨论:①若D点在第一象限,分别过点A、D作y轴的垂线交y轴于点E、F,利用一线三等角可证△ECA≌△FDC,在利用坐标关系求出点D坐标;②若D点在第二象限,原理同①.
解:(1)由平面直角坐标可知:A(1,3),B(-2,-1);
(2)将点A向右平移1个单位到点D,故D点坐标为(2,3),C、B关于y轴对称,故C点坐标为(2,-1),如下图所示:不难发现四边形ABCD为梯形,S梯形ABCD=![]() ;
;
(3)①若D点在第一象限,分别过点A、D作y轴的垂线交y轴于点E、F,如图所示,
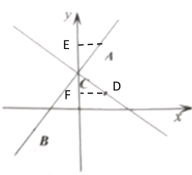
∵△ACD为等腰直角三角形
∴∠ACD=90°,AC=CD
∴∠ECA+∠DCF=90°
又∵∠ECA+∠EAC=90°
∴∠DCF=∠EAC
在△ECA和△FDC中
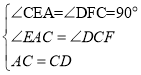
∴△ECA≌△FDC(AAS)
∴EC=DF,AE=CF
设直线AB的解析式为y=kx+b,将A、B代入可得:
![]()
解得![]()
∵直线AB的交y轴于点C
∴点C的坐标为:(0,![]() )
)
∴EC=yA-yC=![]() ,AE=xA=1,
,AE=xA=1,
∴DF=![]() ,CF=1,
,CF=1,
∴FO= yC-CF=![]()
故D点坐标为(![]() ,
,![]() ).
).
②若D点在第二象限,分别过点A、D作y轴的垂线交y轴于点E、F,如图所示
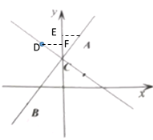
∵△ACD为等腰直角三角形
∴∠ACD=90°,AC=CD
∴∠ECA+∠DCF=90°
又∵∠ECA+∠EAC=90°
∴∠DCF=∠EAC
在△ECA和△FDC中
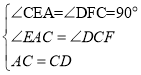
∴△ECA≌△FDC(AAS)
∴EC=DF,AE=CF
利用①中的结论
∴DF=![]() ,CF=1,
,CF=1,
∴FO= yC+CF=![]()
∵点D在第二象限
故D点坐标为(![]() ,
,![]() ).
).
综上所述:D点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() ,点
,点![]() 在直线
在直线![]() 同侧,
同侧,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() 吗?请说明理由;
吗?请说明理由;


(2)如图2,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积
,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积![]() = ;
= ;
(3)如图3,等边![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,动点
,动点![]() 从点
从点![]() 沿射线
沿射线![]() 以
以![]() 速度运动,连结
速度运动,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .请分别求出下列情况点
.请分别求出下列情况点![]() 的运动时间.
的运动时间.
①![]() (直接写出答案);
(直接写出答案);
②点![]() 恰好落在射线
恰好落在射线![]() 上(画出图形,并写出解题过程).
上(画出图形,并写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】20、如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)填空:点A关于X轴对称的点的坐标是 ___,点B关于Y轴对称的点的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个数值转换器,如图所示:

(1)当输入的x为16时.输出的y值是 ;
(2)若输入有效的x值后,始终输不出y值,请写出所有满足要求的x的值,并说明你的理由;
(3)若输出的y是![]() ,请写出两个满足要求的x值: .
,请写出两个满足要求的x值: .
查看答案和解析>>
科目:初中数学 来源: 题型:
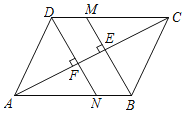
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行了一次“世博”知识竞赛.赛后抽取部分参赛同学的成绩进行整理,并制作成图表如下:

请根据以上图表提供的信息,解答下列问题:
(1)写出表格中m和n所表示的数:m= ,n= ,并补全频数分布直方图;
(2)抽取部分参赛同学的成绩的中位数落在第 组;
(3)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C的坐标分别为(a,0),(0,b),点B在第一象限内,且a,b满足|a3﹣64|+![]() =0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
=0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).

(1)求点B的坐标;
(2)当点P移动4秒时,求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,请直接写出点P移动的时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E.
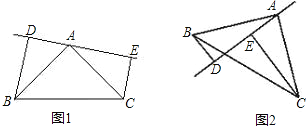
(1)若BC在DE的同侧(如图①)且AD=CE,求证:BA⊥AC.
(2)若BC在DE的两侧(如图②)其他条件不变,问AB与AC仍垂直吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com