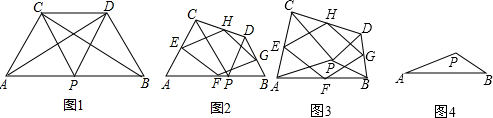
小明数学成绩优秀,他平时善于总结,并把总结出的结果灵活运用到做题中是他成功的经验之一,例如,总结出“依次连接任意一个四边形各边中点所得四边形(即原四边形的中点四边形)一定是平行四边形”后,他想到曾经做过的这样一道题:如图1,点P是线段AB的中点,分别以AP和BP为边在线段AB的同侧作等边三角形APC和等边三角形BPD,连接AD和BC,他想到了四边形ABDC的中点四边形一定是菱形.于是,他又进一步探究:
如图2,若P是线段AB上任一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,设点E,F,G,H分别是AC,AB,BD,CD的中点,顺次连接E,F,G,H.请你接着往下解决三个问题:
(1)猜想四边形ABCD的中点四边形EFGH的形状,直接回答
,不必说明理由;
(2)当点P在线段AB的上方时,如图3,在△APB的外部作△APC和△BPD,其它条件不变,(1)中结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其它条件不变,先补全图4,再判断四边形EFGH的形状,并说明理由.

 阅读快车系列答案
阅读快车系列答案