
【题目】如图1,骰子有六个面并分别标有数1,2,3,4,5,6,如图2,正六边形![]() 顶点处各有一个圈,跳圈游戏的规则为:游戏者掷一次骰子,骰子向上的一面上的数字是几,就沿正六边形的边顺时针方向连续跳几个边长.
顶点处各有一个圈,跳圈游戏的规则为:游戏者掷一次骰子,骰子向上的一面上的数字是几,就沿正六边形的边顺时针方向连续跳几个边长.
如:若从圈![]() 起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈
起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈![]() ;若第二次掷得2,就从
;若第二次掷得2,就从![]() 开始顺时针连续跳2个边长,落到圈
开始顺时针连续跳2个边长,落到圈![]() ;……设游戏者从圈
;……设游戏者从圈![]() 起跳.
起跳.
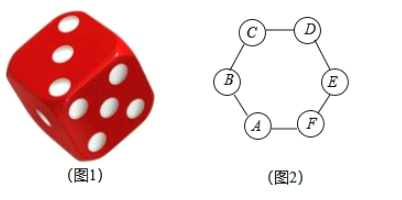
(1)小明随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() ;
;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小明落回到圈
,并指出他与小明落回到圈![]() 的可能性一样吗?
的可能性一样吗?
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )
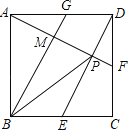
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于( )

A. 1 B. 1.5 C. 2 D. 0.8或1.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡水蜜桃享誉海内外,老王用3000元购进了一批水蜜桃.第一天,很快以比进价高40% 的价格卖出150千克.第二天,他发现剩余的水蜜桃卖相已不太好,于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出,本次生意老王一共获利750元.
(1)根据以上信息,请你编制一个问题,并给予解答;
(2)老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克,第二天,老王把卖相不好的水蜜桃挑出,单独打折销售,售价为10元/千克,结果很快被一抢而空,其余的仍按第一天的价格销售,且当天全部售完.若老王这次至少获利1100元,请问打折销售的水蜜桃最多多少千克?(精确到1千克.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸想给妈妈送张美容卡作为生日礼物,小明家附近有 3 家美容店,爸爸不知 如何选择,于是让小明对 3 家店铺顾客的满意度做了调查:
|
|
| 合计 | |
美容店 A | 53 | 28 | 19 | 100 |
美容店 B | 50 | 40 | 10 | 100 |
美容店 C | 65 | 26 | 9 | 100 |
(说明:顾客对于店铺的满意度从高到低,依次为 3 个笑脸,2 个笑脸,1 个笑脸) 小明选择将_____(填“A”、“ B”或“C”)美容店推荐给爸爸,能使妈妈获得满意体验可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
运动员丙测试成绩的平均数和众数都是7,
(1)成绩表中的![]() __________,
__________,![]() _________;
_________;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从乙手中传出,球传一次甲得到球的概率是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
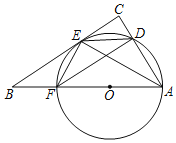
【题目】如图,AF为⊙O的直径,点B在AF的延长线上,BE切⊙O于点E,过点A作AC⊥BE,交BE的延长线交于点C,交⊙O交于点D,连接AE,EF,FD,DE.
(1)求证:EF=ED.
(2)求证:DFAF=2AEEF.
(3)若AE=4![]() ,DE=2
,DE=2![]() ,求sin∠DFA的值.
,求sin∠DFA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com