
【题目】已知∠AOB,作图.
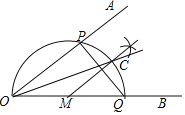
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交弧PQ 于点C;
步骤3:画射线OC.
则下列判断:①弧CQ=弧PC;②MC∥OA;③OP=PQ;④OC平分∠AOB,
其中正确的为_______________(填序号)
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番(“翻一番”表示为原来的2倍)在本世纪的头二十年(2001年~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是![]() ,那么满足的方程为( )
,那么满足的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程kx2-4x+2=0有实数根.
(1)求k的取值范围;
(2)若ABC中,AB=AC=2,AB、BC的长是方程kx2-4x+2=0的两根,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=![]() x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
(1)求抛物线的解析式;
(2)若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地的距离为y1(km),快车离乙地的距离为y2(km),慢车的行驶时间为x(h),两车之间的距离为s(km),y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.
(1)图中的a= ,b= .
(2)从甲地到乙地依次有E,F两个加油站,相距200km,若慢车经过E加油站时,快车恰好经过F加油站,求F加油站到甲地的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表回答问题:
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
(1)272.25的平方根是
(2)![]() = ,
= , ![]() = ,
= , ![]() =
=
(3)设![]() 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一元二次方程![]() 中,若系数
中,若系数![]() 和
和![]() 可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________.
可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com