
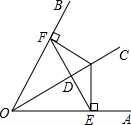
 如图,已知OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,EF交OC于D,则下列结论:
如图,已知OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,EF交OC于D,则下列结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 ①根据角平分线性质得:CE=CF,再证明Rt△OCF≌Rt△OCE,可以得出OE=OF;
②OD与CD不一定相等;
③根据垂直平分线的逆定理得:OC是EF的垂直平分线,则EF⊥OC
④EF不是∠OEC的平分线,所以∠OEF≠∠CEF;
⑤Rt△OCF≌Rt△OCE,同理得:Rt△ODF≌Rt△ODE,Rt△CDF≌Rt△CDE;结论正确.
解答 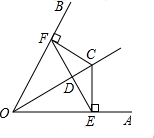 解:①如图,∵OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,
解:①如图,∵OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,
∴CE=CF,
在Rt△OCF和Rt△OCE中,
∵$\left\{\begin{array}{l}{CE=CF}\\{OC=OC}\end{array}\right.$,
∴Rt△OCF≌Rt△OCE(HL),
∴OE=OF;
所以①正确;
②OD与CD不一定相等;所以②不正确;
③∵CE=CF,
∴C是EF垂直平分线上的点,
∵OE=OF,
∴O是EF垂直平分线上的点,
∴OC是EF的垂直平分线,
∴EF⊥OC
所以③正确;
④∵CE=CF,
∴∠CEF=∠CFE
∵OE=OF
∴∠OEF=∠OFE
而∠OEF与∠CEF不一定相等,所以④不正确;
⑤由①可知:Rt△OCF≌Rt△OCE,
同理得:Rt△ODF≌Rt△ODE,Rt△CDF≌Rt△CDE;
所以图中共有3对全等三角形;
所以⑤正确;
综上所述,①③⑤正确,正确的结论一共有3个;
故选B.
点评 本题是三角形的综合题,考查了角平分线、全等三角形的性质、垂直平分线的性质和判定;本题难度不大,属于常考题型;根据角平分线的性质证明边相等,为直角三角形全等创造条件;此题应用了直角三角形特殊的全等判定HL;在证明EF与OC垂直时,可以利用垂直平分线的逆定理,也可以利用三角形全等来证明.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )
如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )| A. | y=-$\frac{\sqrt{3}}{2}$x | B. | y=-$\frac{\sqrt{3}}{3}x$ | C. | y=-$\frac{1}{2}x$ | D. | y=-x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
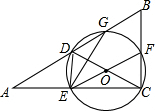 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com