
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
科目:初中数学 来源: 题型:解答题
 阅读下面材料:
阅读下面材料:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点O在线段AB上,AO=1,OB=2,OC为射线,且∠BOC=120°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC作匀速直线运动.设运动时间为t秒,当△ABP为直角三角形时,t的值为( )
如图,点O在线段AB上,AO=1,OB=2,OC为射线,且∠BOC=120°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC作匀速直线运动.设运动时间为t秒,当△ABP为直角三角形时,t的值为( )| A. | t=1 | B. | t=1或$\frac{-1+\sqrt{33}}{8}$ | C. | t=$\frac{1+\sqrt{33}}{8}$ | D. | t=1或$\frac{1+\sqrt{33}}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
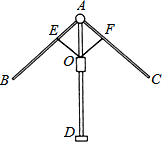 雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{2}$AB,AF=$\frac{1}{2}$AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{2}$AB,AF=$\frac{1}{2}$AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com