
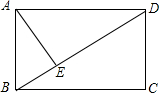
 已知如图,在矩形ABCD中,AE⊥BD,垂足为E,∠ADB=30°且BC=4,则△ECD的面积为________.
已知如图,在矩形ABCD中,AE⊥BD,垂足为E,∠ADB=30°且BC=4,则△ECD的面积为________.
 解:过C点作CF⊥BD于F,
解:过C点作CF⊥BD于F, BC=2,
BC=2, AE=2
AE=2 ,
, ×BF×FC=2
×BF×FC=2 ,
, ,
, .
.

科目:初中数学 来源: 题型:
 若不能,请说明理由.
若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的性质(带解析) 题型:解答题
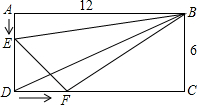
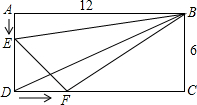
已知如图,在矩形ABCD中,AB=12cm,BC=6cm,点E自A点出发,以每秒1cm的速度向D点前进,同时点F从D点以每秒2cm的速度向C点前进,若移动的时间为t,且0≤t≤6.
(1)当t为多少时,DE=2DF;
(2)四边形DEBF的面积是否为定值?若是定值,请求出定值;若不是定值,请说明理由.
(3)以点D、E、F为顶点的三角形能否与△BCD相似?若能,请求出所有可能的t的值;若不能,请说明理由.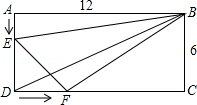
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的性质(解析版) 题型:解答题
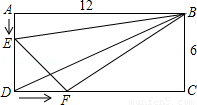
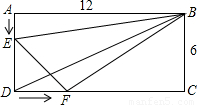
已知如图,在矩形ABCD中,AB=12cm,BC=6cm,点E自A点出发,以每秒1cm的速度向D点前进,同时点F从D点以每秒2cm的速度向C点前进,若移动的时间为t,且0≤t≤6.
(1)当t为多少时,DE=2DF;
(2)四边形DEBF的面积是否为定值?若是定值,请求出定值;若不是定值,请说明理由.
(3)以点D、E、F为顶点的三角形能否与△BCD相似?若能,请求出所有可能的t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 若不能,请说明理由.
若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源:2009-2010学年福建省厦门市一中海沧附属学校九年级(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com