
已知:正比例函数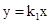 的图象于反比例函数
的图象于反比例函数 的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边的活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:

⑴把上表中(x,y)的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点;
⑵观察所画的图象,猜测y与x之间的函数关系,求出函数关系式并加以验证;
⑶当砝码的质量为24g时,活动托盘B与点O的距离是多少cm?
⑷当活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y=-x+b与反比例函数 的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
(1)、求出b和k;
(2)、求证:△ACD是等腰直角三角形;
(3)、在y轴上是否存在点P,使 ,若存在,请求出P的坐标,若不存在,请说明理由。
,若存在,请求出P的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,正比例函数 的图象与反比例函数
的图象与反比例函数 (
( )的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量
)的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量 的取值范围.
的取值范围.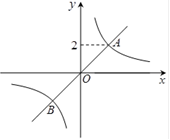
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,一次函数 的图象与反比例函数
的图象与反比例函数 的图象在第一象限内交于点
的图象在第一象限内交于点 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, 。
。
(1)求一次函数和反比例函数的解析式;
(2)若在 轴上存在点
轴上存在点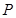 ,使得
,使得 ,求点
,求点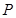 的坐标。
的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,抛物线 的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,函数y1=-x+4的图象与函数y2= (x>0)的图象交于 A(a,1)、B(1,b)两点.
(x>0)的图象交于 A(a,1)、B(1,b)两点.
(1)求a,b及y2的函数关系式;
(2)观察图象,当x>0时,比较y1与y2大小.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com