

分析 (1)根据等腰三角形的性质,可得∠ABC与∠ACB的关系,根据平移的性质,可得AC与DF的关系,根据全等三角形的判定与性质,可得答案;
(2)根据相似三角形的判定与性质,可得GM与HN的关系,BM与FN的关系,根据全等三角形的判定与性质,可得答案.
解答 (1)解:由AB=AC,
得∠ABC=ACB.
由△ABC沿BC方向平移得到△DEF,
得DF=AC,∠DFE=∠ACB.
在△ABF和△DFB中,
$\left\{\begin{array}{l}{AB=DF}\\{∠ABF=∠DFB}\\{BF=FB}\end{array}\right.$,
△ABF≌△DFB(SAS),
BD=AF,
故答案为:BD=AF;
(2)证明:如图: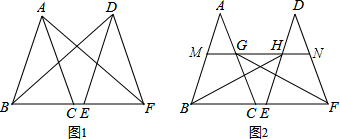 ,
,
MN∥BF,
△AMG∽△ABC,△DHN∽△DEF,
$\frac{MG}{BC}$=$\frac{AM}{AB}$=$\frac{ND}{DF}$,$\frac{HN}{EF}$=$\frac{DN}{DF}$,
∴MG=HN,MB=NF.
在△BMH和△FNG中,
$\left\{\begin{array}{l}{BM=FN}\\{∠BMH=∠FNG}\\{MH=NG}\end{array}\right.$,
△BMH≌△FNG(SAS),
∴BH=FG.
点评 本题考查了全等三角形的判定与性质,利用了平移的性质,相似三角形的判定与性质,全等三角形的判定与性质.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
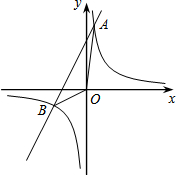 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
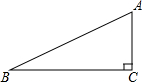 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )| A. | 5÷tan26°= | B. | 5÷sin26°= | C. | 5×cos26°= | D. | 5×tan26°= |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$)
如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com