
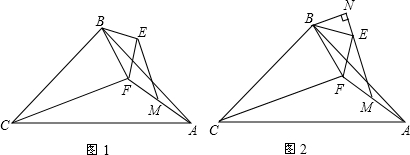
分析 (1)CF与EM的数量关系为CF=2EM;
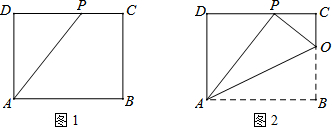
(2)延长FE到点G,使EG=EF,如图1,连结AG、BG,先证明ME为△FAG的中位线得到AG=2ME,再证明△ABG≌△CBF得到AG=CF,于是有CF=2EM;
(3)延长FE到点G,使EG=EF,如图2,连结AG、BG,作FH⊥ME于H,交AG于L,延长BN交AG于K,由△ABG≌△CBF得AG=CF,再证明△FEH≌△EBN得到FH=EN=2,HE=BN=4,利用ME为△FAG的中位线得到FH=HL=2,ME∥AG,接着利用四边形HLKN为矩形得到NK=HL=2,KL=HN=6,所以BK=6,于是利用勾股定理可计算出AK=8,然后求出AG=10,这样可得到CB=CF,则∠CFB=∠CBF,最后利用三角形内角和确定∠CBF与∠BCF之间的数量关系.
解答 (1)解:CF与EM的数量关系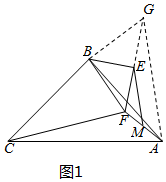 为CF=2EM;
为CF=2EM;
故答案为CF=2EM;
(2)证明:延长FE到点G,使EG=EF,如图1,连结AG、BG,
∵M点为AF的中点,
而EF=EG,
∴ME为△FAG的中位线,
∴AG=2ME,
∵△BEF为等腰直角三角形,
∴∠BEF=90°,BE=EF,
而EF=EG,
∴△BEG为等腰直角三角形,
∴∠BGE=∠EBG=45°,
∴△FBG为等腰直角三角形,
∴BF=BG,∠FBG=90°,
∵∠ABG+∠ABF=90°,∠CBF+∠ABF=90°,
∴∠ABG=∠CBF,
在△ABG和△CBF中
$\left\{\begin{array}{l}{BA=BC}\\{∠ABG=∠CBF}\\{BG=BF}\end{array}\right.$,
∴△ABG≌△CBF,
∴AG=CF,
∴CF=2ME;
(3)延长FE到点G,使EG=EF,如图2,连结AG、BG,作FH⊥ME于H,交AG于L,延长BN交AG于K,
由(2)得△ABG≌△CBF,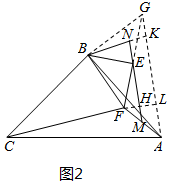
∴AG=CF,
∵∠FEH+∠BEN=90°,∠EBN+∠BEN=90°,
∴∠FEH=∠EBN,
在△FEH和△EBN中
$\left\{\begin{array}{l}{∠FHE=∠BNE}\\{∠FEH=∠EBN}\\{FE=EB}\end{array}\right.$,
∴△FEH≌△EBN,
∴FH=EN=2,HE=BN=4,
∵ME为△FAG的中位线,
∴FH=HL=2,ME∥AG,
易得四边形HLKN为矩形,
∴NK=HL=2,KL=HN=4=2=6,
∴BK=BN+NK=4+2=6,
在Rt△ABK中,BA=BC=10,BK=6,
∴AK=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AL=AK-KL=8-6=2,
∵EH∥GL,EF=EG,
∴GL=2EH=8,
∴AG=AL+LG=2+8=10,
∴AB=AC,
∴CB=CF,
∴∠CFB=∠CBF,
而∠CFB+∠CBF+∠BCF=180°,
∴2∠CBF+∠BCF=180°,
即∠CBF=90°-$\frac{1}{2}$∠BCF.
点评 本题考查了几何变换综合题:熟练掌握旋转的性质和等腰直角三角形的性质;利用线段中点构建三角形中位线得到线段之间的位置关系与数量关系;会利用全等三角形的知识解决线段相等的问题.


科目:初中数学 来源: 题型:解答题
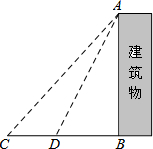 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
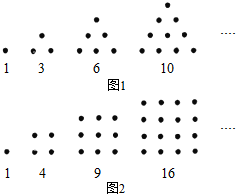 古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数位正方形数(四边形数).
古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数位正方形数(四边形数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com