
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 内角
内角![]() 的平分线,
的平分线,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() 是
是![]() 外角
外角![]() 的平分线,以下结论不正确的是( )
的平分线,以下结论不正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]() 平分
平分![]()
【答案】D
【解析】
A、由AD平分△ABC的外角∠EAC,求出∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD=∠ABC,利用同位角相等两直线平行得出结论正确.
B、由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,得出结论∠ACB=2∠ADB,
C、在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,得出结论∠ADC=90°-∠ABD;
D、由BD平分∠ABC,得到∠ABD=∠DBC,由于∠ADB=∠DBC,∠ADC=90°-![]() ∠ABC,得到∠ADB不等于∠CDB,故错误.
∠ABC,得到∠ADB不等于∠CDB,故错误.
A. ∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故A正确.
B. 由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故B正确.
C. 在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°∠ABD,
故C正确;
D. ∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°![]() ∠ABC,
∠ABC,
∴∠ADB不等于∠CDB,∴D错误;
故选D.


科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=![]() .例如18可分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可分解成1×18,2×9,3×6这三种,这时就有F(18)=![]() =
=![]() .给出下列关于F(n)的说法:
.给出下列关于F(n)的说法:
(1)F(2)=![]() ;(2)F(12)=
;(2)F(12)=![]() ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.
其中正确说法的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(-3,0),B(0,3),DA⊥x轴,点C在OA上且∠CDB=∠ OBD,则∠CBD的度数是( )
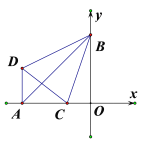
A.72°B.60°C.45°D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB延AE折叠刀AF,延长EF交DC于G,连接AG,现在有如下结论:①∠EAG=45°;②GC=CF;③FC∥AG;④S△GFC=14.4;其中结论正确的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-4,0),B(2,0),C(3,3),反比例函数y=![]() 的图象经过点C.
的图象经过点C.
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形ABC′D′,请说明点D′在双曲线上;
(3)连接AC,CD′,求△ACD′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,0)、B(﹣3,﹣3)、C(0,﹣5)
(1)画出△ABC;
(2)△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+5,y1+3).画出平移后的△A′B′C′,并求△A′B′C′的面积;
(3)设直线A′C′与x轴交于点Q,求交点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组根据学习函数的经验,对函数![]() 的图像和性质进行探究,过程如下:
的图像和性质进行探究,过程如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值如下表:
x | ... | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ... |
y | ... | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | ... |
其中m= .
(2)如图,在平面直角坐标系xoy中,描出了上表中各对对应值为坐标的点,根据描出的点,面出该函数的图象:

(3)根据面出的函数图象特征,仿照示例,完成下列表格中的消数变化规律,
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在y轴左侧,函数图象呈下降状态 | 当x<0时,y随x的增大而减小 |
① | 在y轴右侧,函数图象呈上升状态 | |
示例2 | 函数图象经过点( -4,3) | 当x=-4时,y=3 |
② | 函数图象的最低点是(0,1) |
(4)当2<y<3时,x的取值范图为: ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com