
 (2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为
(2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为| 1 |
| 2 |
| S△ADE |
| S△ABC |
| DE |
| BC |
| 1 |
| 4 |
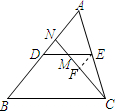 EF=
EF=| 1 |
| 2 |
|
| S△CEF |
| S△CAN |
| EF |
| AN |
| 1 |
| 4 |
| S△DMN |
| S△BCN |
| MN |
| CN |
| 1 |
| 16 |


科目:初中数学 来源: 题型:
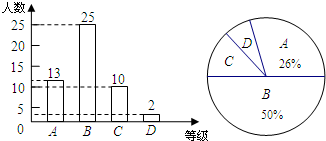 (2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空:
(2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空:查看答案和解析>>
科目:初中数学 来源: 题型:
| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
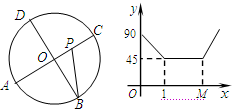 (2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为
(2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com