
【题目】如图,已知抛物线y=x2-(2m+1)x+m2+m-2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,P(s,t)为抛物线上A、B之间一点(不包括A、B),连接AP、BP分别交y轴于点E、D
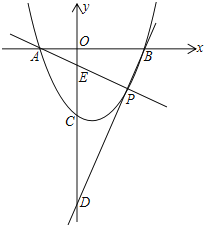
(1)若m=-1,求A、B两点的坐标
(2)若s=1,求ED的长度
(3)若∠BAP=∠ODP,求t的值
【答案】(1)A(-2,0)、B(1,0)(2)3(3) t=-1
【解析】试题分析:(1)把m=-1代入抛物线y=x2-(2m+1)x+m2+m-2得y=x2+x-2,令y=0得方程x2+x-2=0,解得x=-2或x=1,即可得)A(-2,0)、B(1,0);(2)先求得A、B两点的坐标,再表示出点P的坐标,分别求得直线AP、BP的解析式,从而求得DE的长;(3)由∠BAP=∠ODP可得∠DPE=∠AOE=90°,过点P作PQ⊥x轴于Q,由射影定理得,t2=(s-xA)(xB-s),整理得s(xA+xB)-s2-xAxB=t2,根据根与系数的关系可得s·(2m+1)-s2-(m-1)(m+2)=t2,把x=s代入解得t值即可.
试题解析:
(1)A(-2,0)、B(1,0)
(2)∵y=[x-(m+2)][x-(m-1)]
∴A(m-1,0)、B(m+2,0)
∵s=1
∴P(1,m2-m-2)
∴直线AP的解析式为y=-(m+1)x+m2-1
直线BP的解析式为y=-(m-2)x+m2-4
∴DE=m2-1-(m2-4)=3
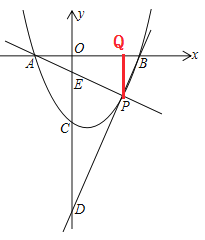
(3) ∵∠BAP=∠ODP
∴∠DPE=∠AOE=90°
过点P作PQ⊥x轴于Q
由射影定理得,t2=(s-xA)(xB-s)
∴s(xA+xB)-s2-xAxB=t2
∴s·(2m+1)-s2-(m-1)(m+2)=t2
当x=s时,t=s2-(2m+1)s+(m-1)(m+2)
∴t2=-t,解得t=-1


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:一般地,n个相同因数a相乘:记为an . 如23=8,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么(log216)2+ ![]() log381= .
log381= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com