
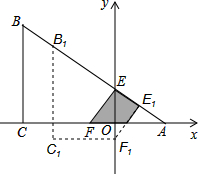
 如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.
如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.分析 (1)运用30°的角的直角三角形求解即可求出折痕EF的长.
(2)存在,作B1D⊥BC,由(1)可得FO的长,进而可求出B1D的长度,在直角三角形中可求出BB1,即x的值.
(3)分4种情况讨论①当0≤x≤2时,即点E到A时经过的面积,②当2<x≤$\frac{10}{3}$时,S为△AEF的面积,③当$\frac{10}{3}$<x≤4时,④当4<x≤6时,根据四边形B1C1F1E1与△AEF重叠的面积为S与x关系求出表达式及自变量x的取值范围.
解答 解:(1)∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∵A($\sqrt{3}$,0),
∴EO=1,
∵∠EFO=60°,∠EOF=90°,
∴EF=$\frac{EO}{sin60°}$=$\frac{2\sqrt{3}}{3}$,
(2)存在,理由如下:
如图1,作B1D⊥BC,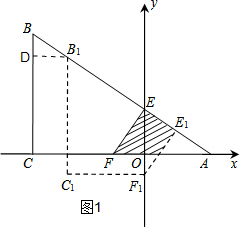
∵FO=$\frac{\sqrt{3}}{3}$,
∴B1D=$\frac{\sqrt{3}}{3}$,∠B=60°
∴BB1=$\frac{{B}_{1}D}{sin60°}$=$\frac{2}{3}$,即x=$\frac{2}{3}$,
(3)①当0≤x≤2时,即点E到A时经过的面积,如图2,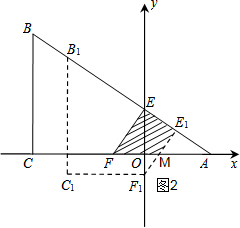
∵AO=$\sqrt{3}$,∠ACB=90°,∠B=60°,
∴AE=2,
∵BB1=EE1=x,
∴E1A=2-x,
∴E1M=$\frac{\sqrt{3}}{3}$(2-x),
∴S=$\frac{1}{2}$(EF+E1M)•E1E=$\frac{1}{2}$[$\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}}{3}$(2-x)]•x=-$\frac{\sqrt{3}}{6}$x2+$\frac{2\sqrt{3}}{3}$x
②当2<x≤$\frac{10}{3}$时,S为△AEF的面积,
所以S=$\frac{1}{2}$EF•AE=$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$×2=$\frac{2\sqrt{3}}{3}$,
③当$\frac{10}{3}$<x≤4时,如图3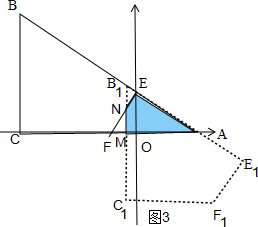
∵∠ACB=90°,∠B=60°,BC=3,
∴AC=3$\sqrt{3}$,
∵AO=$\sqrt{3}$,OF=$\frac{\sqrt{3}}{3}$,
∴CF=3$\sqrt{3}$-$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{5\sqrt{3}}{3}$,
∴此时BB1=$\frac{10}{3}$,即当B1C1过点F时x=$\frac{10}{3}$,
当x>$\frac{10}{3}$时,FM=$\frac{\sqrt{3}}{2}$(x-$\frac{10}{3}$),在RT△NMF中,NM=$\sqrt{3}$FM=$\frac{3}{2}$(x-$\frac{10}{3}$),
∴△NMF的面积为:$\frac{1}{2}$FM•MN=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$(x-$\frac{10}{3}$)×$\frac{3}{2}$(x-$\frac{10}{3}$),
∴S=S△AEF-S△NMF=$\frac{2\sqrt{3}}{3}$-$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$(x-$\frac{10}{3}$)×$\frac{3}{2}$(x-$\frac{10}{3}$)=-$\frac{3\sqrt{3}}{8}$x2+$\frac{5}{2}$x-$\frac{7\sqrt{3}}{2}$,
④当4<x≤6时,如图4,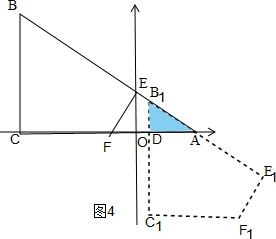
∵∠ACB=90°,∠B=60°,BC=3,
∴AB=6,
AB1=6-x,
∴DB1=$\frac{1}{2}$(6-x),AD=$\frac{\sqrt{3}}{2}$(6-x),
∴S=$\frac{1}{2}$DA•DB1=$\frac{1}{2}$×$\frac{1}{2}$(6-x)×$\frac{\sqrt{3}}{2}$(6-x)=$\frac{\sqrt{3}}{8}$x2-$\frac{3\sqrt{3}}{2}$x+$\frac{9\sqrt{3}}{2}$,
综上可知S与x的函数关系式为:S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{6}{x}^{2}+\frac{2\sqrt{3}}{3}x(0≤x≤2)}\\{\frac{2\sqrt{3}}{3}(2<x≤\frac{10}{3})}\\{-\frac{3\sqrt{3}}{8}{x}^{2}+\frac{5}{2}x-\frac{7\sqrt{3}}{2}(\frac{10}{3}<x≤4)}\\{\frac{\sqrt{3}}{8}{x}^{2}-\frac{3\sqrt{3}}{2}x+\frac{9\sqrt{3}}{2}(4<x≤6)}\end{array}\right.$,
故答案为:S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{6}{x}^{2}+\frac{2\sqrt{3}}{3}x(0≤x≤2)}\\{\frac{2\sqrt{3}}{3}(2<x≤\frac{10}{3})}\\{-\frac{3\sqrt{3}}{8}{x}^{2}+\frac{5}{2}x-\frac{7\sqrt{3}}{2}(\frac{10}{3}<x≤4)}\\{\frac{\sqrt{3}}{8}{x}^{2}-\frac{3\sqrt{3}}{2}x+\frac{9\sqrt{3}}{2}(4<x≤6)}\end{array}\right.$.
点评 本题主要考查了几何变换综合题,涉及直角三角形,梯形面积,三角形面积及坐标轴,第三小题是难点,解题的关键是要分4种情况讨论,本题还考查了分段函数的知识,二次函数的综合运用以及三角函数的应用.难度较大,对学生的计算能力要求很高.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{11}{4}$ | D. | $\frac{\sqrt{26}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
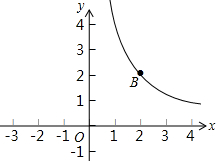 在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(k≠0,x>0)的图象如图所示.已知此图象经过A(m,n),B(2,2)两点.过点B作BD⊥y轴于点D,过点A作AC⊥x轴于点C,AC与BD交于点F.一次函数y=ax+b(a≠0)的图象经过点A、D,与x轴的负半轴交于点E.
在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(k≠0,x>0)的图象如图所示.已知此图象经过A(m,n),B(2,2)两点.过点B作BD⊥y轴于点D,过点A作AC⊥x轴于点C,AC与BD交于点F.一次函数y=ax+b(a≠0)的图象经过点A、D,与x轴的负半轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
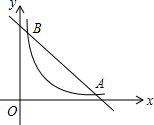 如图,在直角坐标系中,直线y=6-x与双曲线$y=\frac{4}{x}$ (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为4,12.
如图,在直角坐标系中,直线y=6-x与双曲线$y=\frac{4}{x}$ (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为4,12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
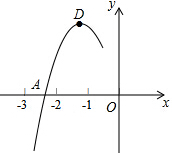 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )| A. | b2-4ac<0 | |
| B. | a+b+c<0 | |
| C. | c-a=2 | |
| D. | 方程ax2+bx+c-2=0有两个相等的实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
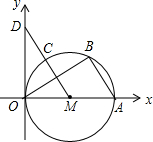 如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.
如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.
如图,已知抛物线y=x2+bx+c经过A(0,-1)、B(4,-3)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com