
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (-$\sqrt{3}$)2=9 | C. | $\root{3}{-9}$=-3 | D. | ±$\sqrt{9}$=±3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
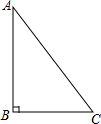 如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )
如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )| A. | $\frac{7}{sin40°}$ | B. | $\frac{7}{tan40°}$ | C. | 7cos40° | D. | $\frac{7}{cos40°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| B. | 数据1、2、2、3的平均数是2 | |
| C. | 数据5、2、-3、0的极差是8 | |
| D. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次一定有4次中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
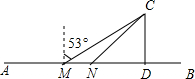 重庆市铜梁区政府为做大乡村旅游,打造了“五朵金花”,其中西边A处有“万亩生态湿地荷花园”,东边B处有“沙心玫瑰园”,为了落实这一举措,区政府计划在A、B两旅游景点之间修建一条公路AB,已知公路AB的一侧有“四季花海”景点C,在公路AB上的M处测得景点C在M的北偏东53°方向上,从M向东走300米到达N处,测得景点C在N的东北方向上,且景点C周围800米范围内为“四季花海”.
重庆市铜梁区政府为做大乡村旅游,打造了“五朵金花”,其中西边A处有“万亩生态湿地荷花园”,东边B处有“沙心玫瑰园”,为了落实这一举措,区政府计划在A、B两旅游景点之间修建一条公路AB,已知公路AB的一侧有“四季花海”景点C,在公路AB上的M处测得景点C在M的北偏东53°方向上,从M向东走300米到达N处,测得景点C在N的东北方向上,且景点C周围800米范围内为“四季花海”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.79×107 | B. | 4.79×108 | C. | 4.79×109 | D. | 4.79×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18 | B. | $\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | ±$3\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com