
分析 根据已知条件得到a2=(a+2b-c)(a-c).b2=(2a+b-c)(b-c).将其代入所求的代数式进行化简即可.
解答 解:∵a2+b2=(a+b-c)2,
∴a2=(a+b-c)2-b2,
=(a+b-c+b)(a+b-c-b)
=(a+2b-c)(a-c).
同理,b2=(2a+b-c)(b-c).
∴$\frac{{a}^{2}+(a-c)^{2}}{{b}^{2}+(b-c)^{2}}$
=$\frac{(a+2b-c)(a-c)+(a-c)^{2}}{(2a+b-c)(b-c)+(b-c)^{2}}$
=$\frac{(a-c)(a+2b-c+a-c)}{(b-c)(2a+b-c+b-c)}$
=$\frac{(a-c)(2a+2b-2c)}{(b-c)(2a+2b-2c)}$
=$\frac{a-c}{b-c}$.
点评 本题考查了约分.约分时,分子与分母都必须是乘积式,如果是多项式的,必须先分解因式.


科目:初中数学 来源: 题型:解答题
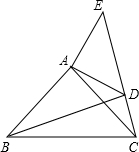 已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D在BC边上,利用直尺与圆规先作∠ACB的平分线,交AD于点F,再作线段AB的垂直平分线,交AB于点E,最后连接EF.
如图,在△ABC中,点D在BC边上,利用直尺与圆规先作∠ACB的平分线,交AD于点F,再作线段AB的垂直平分线,交AB于点E,最后连接EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com