
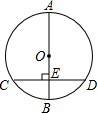
 如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=8,BE=2.求⊙O的半径.
如图,在⊙O中,AB是直径,CD是弦,且AB⊥CD于点E,CD=8,BE=2.求⊙O的半径.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
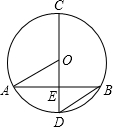 已知:如图,在⊙O中,直径CD交弦AB于点E,且CD平分弦AB,连接OA,BD.
已知:如图,在⊙O中,直径CD交弦AB于点E,且CD平分弦AB,连接OA,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.
如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
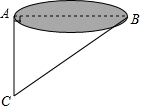 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.| A. | 75•sin55° | B. | 75•cos55° | C. | 75•tan55° | D. | $\frac{75}{tan55°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
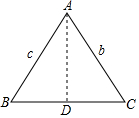 利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)
利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com