
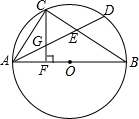
 AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF.
AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF. 分析 ①连接CD,根据同弧所对的圆周角相等得到∠ABC=∠ADC=∠ACD,根据∠ACF+∠GCE=90°,∠CAD+∠GEC=90°,得到答案;
②延长CF交⊙O于H,由①证得∠ACH=∠CAD,于是得到$\widehat{AH}$=$\widehat{CD}$,$\widehat{CH}$=$\widehat{AD}$,根据圆心角、弧、弦之间的关系得到AD=CH,根据垂径定理得到CH=2CF,等量代换即可得到结论.
解答 证明:①连接CD,
∵C是$\widehat{AD}$的中点,
∴∠ABC=∠ADC=∠CAD,
∵AB为直径,∴∠ACB=90°,CF⊥AB,
∴∠ACF=∠ABC,
∴∠ACF=∠CAD,
∴AG=CG,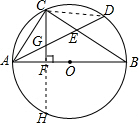
∵∠ACF+∠GCE=90°,∠CAD+∠GEC=90°,
∴∠GCE=∠GEC,
∴CG=EG,
∴CG=EG=AG;
②延长CF交⊙O于H,
由①证得∠ACH=∠CAD,
∴$\widehat{AH}$=$\widehat{CD}$,
∴$\widehat{CH}$=$\widehat{AD}$,
∴AD=CH,
∵AB是⊙O的直径,CF⊥AB,
∴CH=2CF,
∴AD=2CF.
点评 本题考查的是圆周角定理,垂径定理,等腰三角形的判定和性质,圆心角、弧、弦之间的关系,掌握同弧所对的圆周角相等、直径所对的圆周角等于90°是解题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形纸片ABCD中,BC=10,CD=8,如图,折叠纸片,试点A落在BC边上的A′处,折痕为PQ,当A′在BC上运动时,折痕的端点P,Q也随之移动.若限定Q只能在AD上移动,则线段PQ的最小值为5$\sqrt{5}$.
如图,在矩形纸片ABCD中,BC=10,CD=8,如图,折叠纸片,试点A落在BC边上的A′处,折痕为PQ,当A′在BC上运动时,折痕的端点P,Q也随之移动.若限定Q只能在AD上移动,则线段PQ的最小值为5$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形ABCD的上底为4,下底为6,高为3,它是由梯形A′,B′,C′,D′经过轴对称变换而来的,已知对称轴为x轴,写出A′,B′,C′,D′的坐标.
如图,梯形ABCD的上底为4,下底为6,高为3,它是由梯形A′,B′,C′,D′经过轴对称变换而来的,已知对称轴为x轴,写出A′,B′,C′,D′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
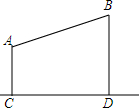 因需要,计划在山顶A,B处架绳索设一绳索滑道.已测到山顶A的海拔高度AC为300米,山顶B的海拔高度BD为800米,山顶A,B之间的水平宽度CD为1200米,问这一绳索至少需要多少米?
因需要,计划在山顶A,B处架绳索设一绳索滑道.已测到山顶A的海拔高度AC为300米,山顶B的海拔高度BD为800米,山顶A,B之间的水平宽度CD为1200米,问这一绳索至少需要多少米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知⊙O的半径为r.
已知⊙O的半径为r.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com