
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=kx上,则(1)k=$\frac{\sqrt{3}}{3}$,(2)A2015的坐标是(2015$\sqrt{3}$,2017).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=kx上,则(1)k=$\frac{\sqrt{3}}{3}$,(2)A2015的坐标是(2015$\sqrt{3}$,2017). 分析 (1)先根据等边三角形的性质求出∠1的度数,过B1向x轴作垂线B1C,垂足为C,求出B1点的坐标.利用待定系数法求出直线y=kx的解析式即可;
(2)根据题意得出直线AA1的解析式为:y=$\frac{\sqrt{3}}{3}$x+2,进而得出A,A1,A2,A3坐标,进而得出坐标变化规律,进而得出答案.
解答  解:(1)∵△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,
解:(1)∵△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,
∴∠1=30°.
过B1向x轴作垂线B1C,垂足为C,
∵OB1=2,
∴CB1=1,OC=$\sqrt{3}$,
∴B1($\sqrt{3}$,1),
∴1=$\sqrt{3}$k,解得k=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{{\sqrt{3}}}{3}$;
(2)∵由(1)知,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,
∴A(0,2),AO∥A1B1,∠B1OC=30°,
∴CO=OB1cos30°=$\sqrt{3}$,
∴B1的横坐标为:$\sqrt{3}$,则A1的横坐标为:$\sqrt{3}$,
连接AA1,可知所有三角形顶点都在直线AA1上,
∵点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,AO=2,
∴直线AA1的解析式为:y=$\frac{\sqrt{3}}{3}$x+2,
∴y=$\frac{\sqrt{3}}{3}$×$\sqrt{3}$+2=3,
∴A1($\sqrt{3}$,3),
同理可得出:A2的横坐标为:2$\sqrt{3}$,
∴y=$\frac{\sqrt{3}}{3}$×2$\sqrt{3}$+2=4,
∴A2(2$\sqrt{3}$,4),
∴A3(3$\sqrt{3}$,5),
…
A2015(2015$\sqrt{3}$,2017).
故答案为:(2015$\sqrt{3}$,2017).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 79.9×108 | B. | 7.99×108 | C. | 7.99×105 | D. | 0.799×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
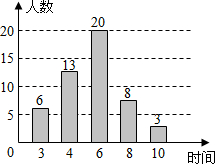 为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )| A. | 6,4 | B. | 6,6 | C. | 4,4 | D. | 4,6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com