
【题目】如图,已知AB是⊙O的直径,BC是⊙O的切线,连接AC与⊙O交于点 D.取BC的中点E,连接DE,并连接OE交⊙O于点F.连接AF交BC于点G,连接BD交AG于点H.
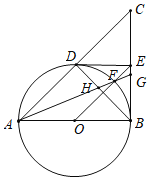
(1)若EF=1,BE=![]() ,求∠EOB的度数;
,求∠EOB的度数;
(2)求证:DE为⊙O的切线;
(3)求证:点F为线段HG的中点.
【答案】(1)∠EOB=60°;(2)见解析;(3)见解析.
【解析】
(1)根据切线的性质得到∠ABC=90°,解直角三角形得到∠EOB=60°;
(2)连结OD,根据圆周角定理得到∠ADB=∠BDC=90°,求得DE=EC,根据切线的判定定理即可得到结论;
(3)根据三角形的中位线的性质得到OE∥AC,根据平行线的性质得到OE⊥BD,得到![]() ,求得∠FBD=∠FAB,根据等腰三角形的性质即可得到结论.
,求得∠FBD=∠FAB,根据等腰三角形的性质即可得到结论.
(1)∵AB是⊙O的直径,BC是⊙O的切线,
∴∠ABC=90°,
在直角三角形OBE中,设圆O半径为r,
∵EF=1,BE=![]() ,则,r2+(
,则,r2+(![]() )2=(r+1)2,
)2=(r+1)2,
解得r=1,
∴OB=1,OE=2,
在Rt△OBE中,cos∠EOB=![]() ,
,
∴∠EOB=60°;
(2)连结OD,
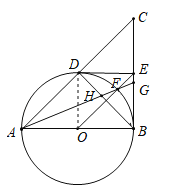
∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°,
∵E为直角三角形BCD斜边的中点,
∴DE=EC,
∴∠CDE=∠C,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠ODA+∠CDE=∠OAD+∠C=90°,
∴∠ODE=180°﹣90°=90°,
∴DE是⊙O的切线;
(3)连接BF,
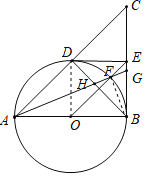
∵AB是圆O的直径,
∴∠AFB=90°,即BF⊥AF,
∵O、E分别为AB、BC的中点,
∴OE∥AC,
∵BD⊥AC,
∴OE⊥BD,
∴![]() ,
,
∴∠DOF=![]()
∵∠BAF=![]()
∴∠BAF=∠DOF,
∵∠DOF=∠DBF,
∴∠DBF=∠BAF,
∵BC是⊙O的切线,
∴∠EBF+∠ABF=90°
∵∠BAF+∠ABF=90°
∴∠EBF=∠BAF
∴∠EBF=∠HBF
∵BF⊥HG,
∴BF垂直平分HG,
即:点F为线段HG的中点.


科目:初中数学 来源: 题型:
【题目】定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。如图,我们可以看作正六边形的环状连接,中间围成一个边长相等的正六边形;若正八边形作环状连接,中间可以围的正多边形的边数为;

若正八边形作环状连接,中间可以围的正多边形的边数为________,若边长为1的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (
(![]() ).
).
(1)写出抛物线顶点的纵坐标 (用含a的代数式表示);
(2)若该抛物线与x轴的两个交点分别为点A和点B,且点A在点B的左侧,AB=4.
①求a的值;
②记二次函数图象在点A,B之间的部分为W(含点A和点B),若直线![]() (
(![]() )经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
)经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
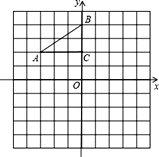
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
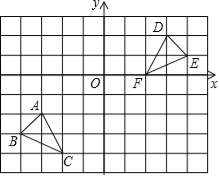
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC向上平移4个单位长度后所得到的△A1B1C1;
(2)画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1;
(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形吗?如果是,请直接写出对称轴所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学课外小组,在坐标纸上为某湿地公园的一块空地设计植树方案如下:第k棵树种植在点Pk(xk,yk)处,其中x1=1,y1=1,且k≥2时,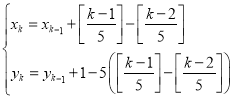 ,[a]表示非负实数a的整数部分,例如[2.3]=2,
,[a]表示非负实数a的整数部分,例如[2.3]=2,![]() ,[0.5]=0.按此方案,第2019棵树种植点的坐标应为( )
,[0.5]=0.按此方案,第2019棵树种植点的坐标应为( )
A.(6,2020)B.(2019,5)C.(3,403)D.(404,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
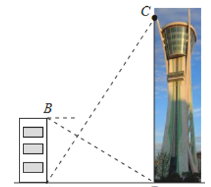
【题目】为测量观光塔高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,请根据以上观测数据求观光塔的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
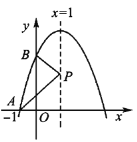
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x轴、y轴的交点分别为A,B,点P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0;②x=3是ax2+bx+3=0的一个根;③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是________.
.其中正确的是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com