练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，OA∶OD∶OC∶OB＝2∶2∶3∶4，求(S△AOD＋S△OBC)∶(SABO＋SCDO)．

    答案：
    解析：

    　　解：因为OA∶OD∶OC∶OB＝2∶2∶3∶4，

    　　由三角形的性质可知S△AOD∶S△AOB＝2∶4，

    　　设S△AOD＝2x，则S△AOB＝4x，SOBC＝6x，S△DOC＝3x，

    　　所以S△AOD＋S△COB＝2x＋6x＝8x，S△AOB＋S△COD＝4x＋3x＝7x，

    　　所以(S△AOD＋S△COB)∶(S△AOB＋S△COD)＝8x∶7x＝8∶7．

    　　分析：本题只给出图形中四条线段的比值，解这个题的关键是运用三角形面积的性质：若两个三角形高相同(或相等)，则其面积比即为高所对的底边之比．设△ABD的高为h，则h也是△ABO，△ADO的高．因为BO∶OD＝4∶2，所以S△AOB∶S△AOD＝4∶2，设S△AOD＝2x，则S△AOB＝4x，在△ABC中，OA∶OC＝2∶3，则S△AOB∶S△BOC＝2∶3，所以S△BOC＝6x，同理S△DOC＝3x，所以S△AOD＋S△OBC＝2x＋6x＝8x，S△AOB＋S△DOC＝4x＋3x＝7x，所以(S△AOD＋S△OBC)∶(S△OAB＋S△DOC)＝8x∶7x＝8∶7．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图所示，OA=OD，OB=OC，请说明下列结论成立的理由：
    （1）△AOB≌△DOC； 
    （2）AB∥CD．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年浙江省湖州市六校联考八年级上学期期末考试数学试卷（带解析） 题型：计算题

    （6分）如图所示，OA=OD，OB=OC，请说明下列结论成立的理由：

    (1）△AOB≌△DOC； (2）AB∥CD

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年浙江省湖州市六校联考八年级上学期期末考试数学试卷（解析版） 题型：解答题

    （6分）如图所示，OA=OD，OB=OC，请说明下列结论成立的理由：

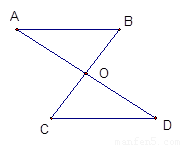
    (1）△AOB≌△DOC； (2）AB∥CD

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图所示，OA=OD，OB=OC，请说明下列结论成立的理由：
    （1）△AOB≌△DOC；
    （2）AB∥CD．

    查看答案和解析>>

    同步练习册答案