
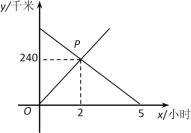
【题目】甲、乙二人驾车分别从A,B两地同时出发,相向而行.下图是二人离A地的距离y(千米)与所用时间x(小时)的关系.
(1)请说明交点P所表示的实际意义: ;
(2)试求出A,B两地之间的距离;
(3)甲从A地到达B地所需的时间为多少?
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
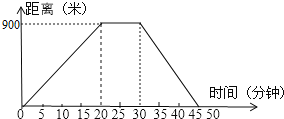
【题目】如图,反映了小明从家里到超市的时间与距离之间关系的一幅图。
(1)图中自变量和因变量各是什么?
(2)小明到达超市用了多少时间?超市离家多远?
(3)分别求小明从家里到超市时的平均速度是多少?返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学课上,老师要求学生根据图中李亮与张鑫的对话内容,展开如下活动:
仔细阅读对话内容:

活动:根据对话内容,提出一些数学问题,并解答.
下面是学生提出的两个问题,请你列方程解答.
(1)如果张鑫没有办卡,他需要付多少钱;
(2)你认为购买多少元钱的书时办卡与不办卡花费相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.
(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
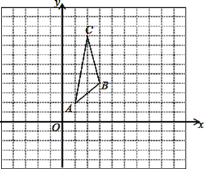
【题目】在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)直接写出△ABC上点M(x,y)在上述变换过程中得到的对应点M2的坐标.
(3)直接写出△A1B1C1关于x轴对称后三个顶点A2、B2、C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在期末考试来临之际,同学们都进入紧张的复习阶段,为了了解同学们晚上的睡眠情况,现对年级部分同学进行了调查统计,并制成如下两幅不完整的统计图:(其中A代表睡眠时间8小时左右,B代表睡眠时间6小时左右,C代表睡眠时间4小时左右,D代表睡眠时间5小时左右,E代表睡眠时间7小时左右),其中扇形统计图中“E”的圆心角为90°,请你结合统计图所给信息解答下列问题:
(1)共抽取了 名同学进行调查,同学们的睡眠时间的中位数是 小时左右,并将条形统计图补充完整;
(2)请你估计年级每个学生的平均睡眠时间约多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
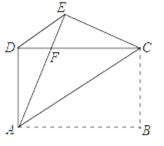
【题目】如图,在长方形ABCD中,AB>BC,把长方形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE
求证:(1)△AED≌△CDE
(2)△EFD是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com