
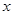 .
.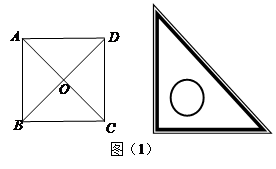 ,并说明理由。
,并说明理由。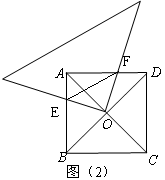
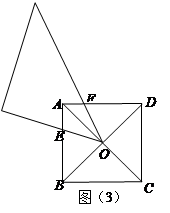
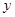 ,求
,求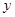 关于
关于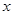 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;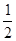 x2-2x+4 (3)EF与正方形ABCD的内切圆相切。
x2-2x+4 (3)EF与正方形ABCD的内切圆相切。 ,BO=AO=OD,
,BO=AO=OD, ∴∠AOF=∠BOE∴△AOF≌△BOE
∴∠AOF=∠BOE∴△AOF≌△BOE
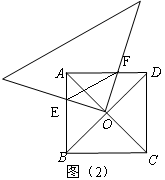
 ∴
∴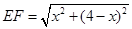
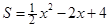
 ∴∠FOD+∠EOB=∠BEO+∠EOB=
∴∠FOD+∠EOB=∠BEO+∠EOB=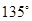
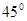 ∴△BOE∽△DFO
∴△BOE∽△DFO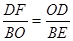 ∴
∴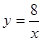
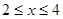 )
)
 ∵BO=DO
∵BO=DO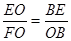 而∠EOF=∠0BE=
而∠EOF=∠0BE=


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源:不详 题型:单选题
| A.6条 | B.3条 | C.4条 | D.5条 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
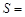 ,△EFC的面积
,△EFC的面积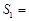 ,△ADE的面积
,△ADE的面积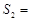 .
.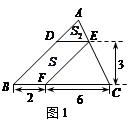
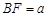 ,
,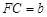 ,DE与BC间的距离为
,DE与BC间的距离为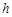 .请证明
.请证明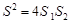 .
.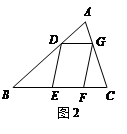
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
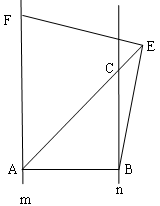
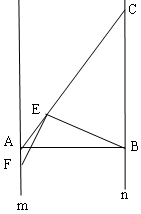
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
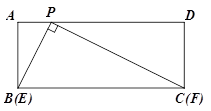
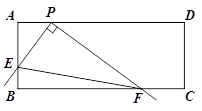
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com