
已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.

科目:初中数学 来源: 题型:
 已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y=
已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y=
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年江苏省常州市中考数学试卷 题型:解答题
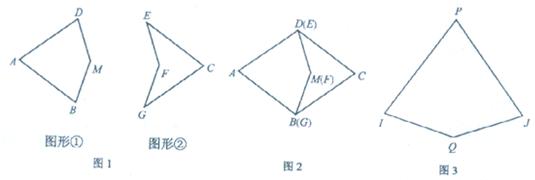
(2011•常州)已知:如图1,图形①满足AD=AB,MD=MB,∠A=72°,∠M=144°.图形②与图形①恰好拼成一个菱形(如图2).记AB的长度为a,BM的长度为b.
(1)图形①中∠B= 72 °,图形②中∠E= 36 °;
(2)小明有两种纸片各若干张,其中一种纸片的形状及大小与图形①相同,这种纸片称为“风筝一号”;另一种纸片的形状及大小与图形②相同,这种纸片称为“飞镖一号”.
①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形,需要这种纸片 5 张;
②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”(如图3),其中∠P=72°,∠Q=144°,且PI=PJ=a+b,IQ=JQ.请你在图3中画出拼接线并保留画图痕迹.(本题中均为无重叠、无缝隙拼接)
查看答案和解析>>
科目:初中数学 来源:2011年江苏省常州市中考数学试卷 题型:解答题
(2011•常州)已知:如图1,图形①满足AD=AB,MD=MB,∠A=72°,∠M=144°.图形②与图形①恰好拼成一个菱形(如图2).记AB的长度为a,BM的长度为b.
(1)图形①中∠B= 72 °,图形②中∠E= 36 °;
(2)小明有两种纸片各若干张,其中一种纸片的形状及大小与图形①相同,这种纸片称为“风筝一号”;另一种纸片的形状及大小与图形②相同,这种纸片称为“飞镖一号”.
①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形,需要这种纸片 5 张;
②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”(如图3),其中∠P=72°,∠Q=144°,且PI=PJ=a+b,IQ=JQ.请你在图3中画出拼接线并保留画图痕迹.(本题中均为无重叠、无缝隙拼接)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com