Question

如图，长方形制片ABCD中，AB=8cm，AD=6cm，按下列步骤进行裁减和拼图

第一步：如图①，在线段AD上任意取一点E，沿EB，EC剪下一个三角形纸片EBC（余下部分不再使用）；
第二步：如图②，沿三角形EBC的中位线GH将纸片剪成两部分，并在线段GH上任意取一点M，线段BC上任意取一点N，沿MN将梯形纸片GBCH剪成两部分；
第三步：如图③，将MN左侧纸片绕G点按顺时针方向旋转180°，使线段GB与GE重合，将MN右侧纸片绕H点按逆时针方向旋转180°，使线段HC与HE重合，拼成一个与三角形纸片EBC面积相等的四边形纸片．（注：裁剪和拼图过程均无缝且不重叠）
（1）所拼成得四边形是什么特殊四边形？
（2）则拼成的这个四边形纸片的周长的最小值是多少？

Answer 1

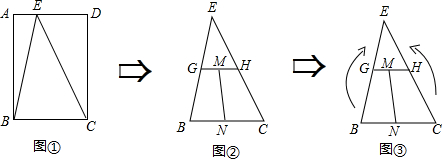
解：（1）画出第三步剪拼之后的四边形M₁N₁N₂M₂的示意图，如答图1所示．
图中，N₁N₂=EN₁+EN₂=NB+NC=BC，
M₁M₂=M₁G+GM+MH+M₂H=2（GM+MH）=2GH=BC（三角形中位线定理），
又∵M₁M₂∥N₁N₂，
∴四边形M₁N₁N₂M₂是一个平行四边形，

（2）其周长为2N₁N₂+2M₁N₁=2BC+2MN．
∵BC=6cm为定值，
∴四边形的周长取决于MN的大小．
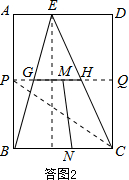
如答图2所示，是剪拼之前的完整示意图，
过G、H点作BC边的平行线，分别交AB、CD于P点、Q点，
则四边形PBCQ是一个矩形，这个矩形是矩形ABCD的一半，
∵M是线段PQ上的任意一点，N是线段BC上的任意一点，
根据垂线段最短，得到MN的最小值为PQ与BC平行线之间的距离，即MN最小值为4cm．
分析：（1）首先确定剪拼之后的四边形是个平行四边形；
（2）根据周长大小取决于MN的大小，然后在矩形中探究MN的不同位置关系，得到其长度的最大值与最大值，从而问题解决．
点评：此题主要考查了图形的剪拼以及考查了动手操作能力和空间想象能力，确定剪拼之后的图形，并且探究MN的不同位置关系得出四边形周长的最值是解题关键．